Pythagorean Triples: a2 + b2 = (b + 1)2

So I wanted to find a quick way to find the Pythagorean Triples for right triangles, which had the smallest leg 9, 11, 13, etc. Simply substituting (b+1) in the Pythagorean Theorem in place of c, I could solve for b in terms of a. Then adding 1 to the expression of b yields an expression for c.

a2 + b2 = (b + 1)2 a2 + b2 = b2 + 2b + 1 a2 = 2b + 1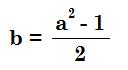

c = b + 1 c = (1/2)(a2 - 1) + 1 c = (1/2)(a2 + 1)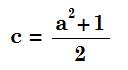

Look at the eqaution a² = 2b + 1 again.

This spurred my curiosity. Or rather it was the result that I was looking for after a student used an incorrect procedure and yet solved three out of five right triangle problems correctly.

When given a leg and the hypotenuse, the student knew that to find the other leg, squaring and subtraction were involved, but didn't have the idea down pat.

To solve 5-__-13, he squared 5, getting 25, and subtracted 13, getting 12, which is the correct answer, He did the same thing for four other problems.

The "method" works for triangles in the form a² + b² = (b + 1)², when looking for b or b + 1.

If b = a² - c (which was the method used)
b = a² - (1/2)(a² + 1
and therefore

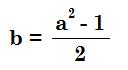
which is the condition that must be true for the method to work.

Okay, I admit, I'm rambling a bit, but when the "method" worked 3 out of 5 times, I needed to know why it had worked then and under what conditions it would work again. And given what I know now, it would be hard to fault the "logic" behind it if one recognized the pattern in the numbers. I'm fairly certain that the student didn't see any pattern here, which explains the two wrong answers, but it did point me back in the direction of finding better examples to use to better ascertain if they understood the work.