
(C)Copyright 2017, C. Burke.
Sometimes you just have to surprise people
Or get replaced with a pod person.
Come back often for more funny math and geeky comics.


Sometimes you just have to surprise people
Or get replaced with a pod person.
Come back often for more funny math and geeky comics.


Westward leading, still proceeding.
A Merry Christmas to all my followers and a Happy Holiday Season.
Come back often for more funny math and geeky comics.


They were a long way from the fjords.
Technical problems kept this from being posted on Friday. Oopsie. At least it made it before Christmas!
Come back often for more funny math and geeky comics.


Happy Aluminum Hydroxide Day!
No, I couldn't wait for December 26.
Come back often for more funny math and geeky comics.


Answer the call!
Which turns out to be "Be There or Be Square Dancing!"
Come back often for more funny math and geeky comics.

It's still morning? How is it still morning? What period is this?
Come back often for more funny math and geeky comics.

Are you sure? Are you positive?
Come back often for more funny math and geeky comics.


The total sum of the entire crew is nothing in the vast emptiness of space.
Come back often for more funny math and geeky comics.


If a terrabyte has a trillion bytes, how many sides does a tarragon have?
Apologies if I've done this one before. It's been "in the notebook" for ages.
Come back often for more funny math and geeky comics.


Obviously, she's already planning on what to get named after her. Ambition is good.
Giovanni Ceva's birthday being today is actually coincidental to the topic coming up in the first place.
Come back often for more funny math and geeky comics.


If you're not there, you're absent.
Come back often for more funny math and geeky comics.


Just watch out for those cubics trying to come between them!
Come back often for more funny math and geeky comics.


That sums it up.
Come back often for more funny math and geeky comics.


Now I have to work on ''Round Me, Mama" ... but don't hold your breath.
Come back often for more funny math and geeky comics.


Integrate Turkey into your holiday dinner! Plus a side dish!
Come back often for more funny math and geeky comics.

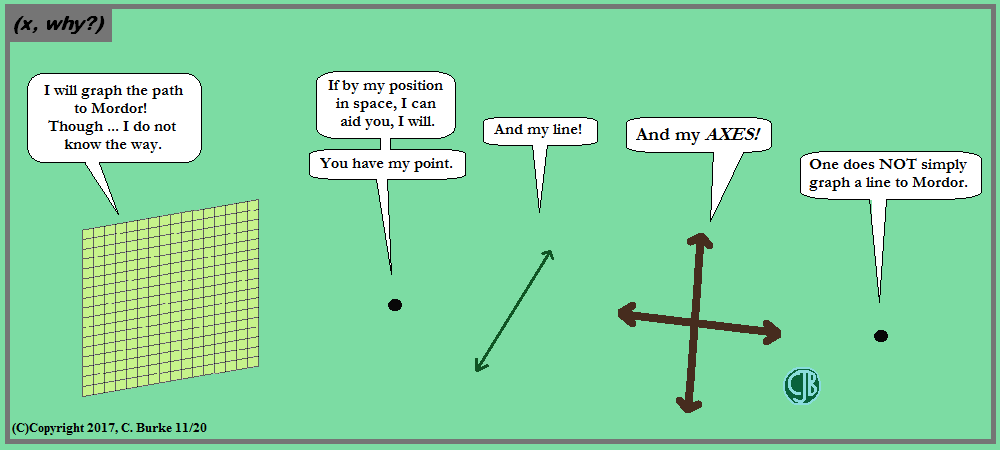
They could have gotten to Mordor quicker if they had taken a plane.
But it doing it was easy, we'd all be soaring on wings of Eagles.
Come back often for more funny math and geeky comics.

I recently realized that I hadn't gotten around to writing up the August 2017 Algebra 1 Regents, so let me start with the multiple choice.
1. A part of Jennifer’s work to solve the equation
(4) distributive property of multiplication over subtraction
2. Which value of x results in equal outputs for j(x) = 3x – 2 and b(x) = |x + 2|?
(2) 2
3. The expression 49x2 - 36 is equivalent to
(3) (7x – 6)(7x + 6)
4. If f(x) = ½ x2 - (1/4 x + 3), what is the value of f(8)?
(3) 27
5. The graph below models the height of a remote-control helicopter over 20 seconds during flight.
(2) 5 to 10 seconds
6. In the functions f(x) = kx2 and g(x) = |kx|, k is a positive integer. If k is replaced by 1/2, which statement about these new functions is true?
(1) The graphs of both f(x) and g(x) become wider.
7. Wenona sketched the polynomial P(x) as shown on the axes below. (1) P(x) = (x + 1)(x - 2)2
8. Which situation does not describe a causal relationship?
(2) The faster a student types a research paper, the more pages the paper will have.
9. A plumber has a set fee for a house call and charges by the hour for repairs. The total cost of her services can be modeled by c(t) = 125t + 25. Which statements about this function are true?
(4) I, II, and III.
10. What is the domain of the relation shown below?
(1) {0, 1, 4}
11. What is the solution to the inequality 2 + (4/9)x > 4 + x?
(1) x < -18/5
August 2017, Algebra 1 (Common Core), Part I
12x2 - 6 = 11x2 - x
The distributive property says to multiply both the 6 and the 3 inside the parentheses by the 2 on the outside.
Since it’s multiple choice, you can just substitute each choice into the two functions. If you don’t like fractions, save it for last, and you might not need it. (In this case you won’t.)
j(2) = 3(2) -2 = 6 – 2 = 4, and b(2) = |2 + 2| = |4| = 4.
Difference of Squares Rule. Again, if you aren’t sure, or don’t remember how to factor the binomial, you can multiply the choices. Choice (1) will have a middle term of 84x and the constant term will be negative. In choices (2) and (4), 24.52 is not equal to 49. Choice (3) remains.
This can be put directly into your calculator in one shot:
1 / 2 * (8)2 - (1 / 4 * (8) + 3), which is 27.

Over which interval does the helicopter have the slowest average rate of change?
Between 5 and 10 seconds the helicopter only rises1 foot. There is a greater average change in all the over five-second intervals.
A leading coefficient of greater than 1 (such as any positive integer greater than 1) will cause a parabola or an absolute value function to become more narrow. On the other hand, a fraction between 0 and 1 will cause the graphs to become wider. Since 1/2 is a smaller value than any positive integer, the graphs will be wider.

Which equation could represent P(x)?
Once again, you can graph these in your calculator if you aren't sure. The curve is cubic, which means that the highest power is 3. Choices 3 and 4 are only quadratic, so they can be eliminated.
The zeroes of the function occur, according to the graph, and x = -1 and x = 2. Choice 1 has those values as zeroes: (-1 + 1) = 0 and (2 - 2) = 0.
The student may be able to produce more pages in a shorter amount of time but there's no reason that he or she will produce more pages as a result.
Also, please make sure you are reading this as "causal" as in "cause and effect" and not as "casual" as in "relaxed and unconcerned".
I. A house call fee costs $95.
II. The plumber charges $125 per hour.
III. The number of hours the job takes is represented by t.
Practically a definition of a function. The variable is time, which is t, and the repeating value is the $125 per hour, which is the coefficient of time. The set fee, which is only charged once, is the "+ 95".
The domain is comprised of the x-values, without repeats. In case you were wondering, this relation is not a function because of the repeating x-values.
12. Konnor wants to burn 250 Calories while exercising for 45 minutes at the gym. On the treadmill, he can burn 6 Cal/min. On the stationary bike, he can burn 5 Cal/min. If t represents the number of minutes on the treadmill and b represents the number of minutes on the stationary bike, which expression represents the number of Calories that Konnor can burn on the stationary bike?
(2) 5b
There is a lot of unneeded information in this problem (although it could be useful in a more complex followup question). The number of minutes on the bike is b and the number of calories per minute is 5. Therefore the amount of calories burned is 5b.
13. Which value of x satisfies the equation (5/6)[(3/8) - x] = 16?
(2) -18.825
I'll leave the factors in until the end. At that point, you can put the entire expression into a calculator in one shot and not worry about interim mistakes.
14. If a population of 100 cells triples every hour, which function represents p(t), the population after t hours?
(2) p(t) = 100(3)t.
The initial value is 100, the base is 3 and the exponent is t. If it triples every hour, it is an exponential function, which eliminate choices 3 and 4, which are both linear.
15. A sequence of blocks is shown in the diagram below.
This sequence can be defined by the recursive function a1 = 1 and an = an-1 + n. Assuming the pattern continues, how many blocks will there be when n = 7?
(3) 28
The sum of 1+2+3+4+5+6+7 = 28, which is a triangular number. You might remember that the 7th triangular number is (7)(8)/2, and that any triangular number is (n)(n+1)/2. If you didn't, it's not a big deal because adding the numbers from 1 to 7 is simple enough.
16. Mario's $15,000 car depreciates in value at a rate of 19% per year. The value, V, after t years can be modeled by the function V = 15,000(0.81)t. Which function is equivalent to the original function?
(2) V = 15,000(0.9)2t.
0.92 = 0.81, so 0.92t = 0.81t.
17. The highest possible grade for a book report is 100. The teacher deducts 10 points for each day the report is late. Which kind of function describes this situation?
(1) linear. The rate of change is -10 per day, not -10%, so it's linear and not exponential decay.
18. The function h(x), which is graphed below, and the function g(x) = 2|x + 4| - 3 are given.
Which statements about these functions are true?
I. g(x) has a lower minimum value than h(x).
II. For all values of x, h(x) < g(x).
III. For any value of x, g(x) =/= h(x).
(2) I and III, only.
The minimum for h(x) is 2 and occurs at (-4, 2). The minimum for g(x) is -3, and occurs at (-4, -3).
You have the option of graphing g(x) and checking the value if you didn't realize that g(x) is in
y = a|x - h| + k, where (h, k) is the minimum point. I is true. This eliminates (3).
Since g(x) < h(x) at x = -3, we know that II is false. This eliminates (1) and (4).
The slope of h(x) in the given graph is -2 on the left and +2 on the right. In g(x), the slope is -2 when x < -4 and 2 when x > -4, so the graphs are parallel and will never be equal. Therefore III is true.
18. The zeros of the function f(x) = 2x3 + 12x - 10x2 are
(3) {0, 2, 3}.
Several methods. First, put it in your graphing calculator and check the Tables of Values.
Second, immediately realize that 0 is a solution because each of the terms has a x in it, which eliminates choices (1) and (2), and then enter the following in your calculator
20. How many of the equations listed below represent the line passing through the points (2, 3) and (4, -7)?
5x + y = 13
y + 7 = -5(x - 4)
y = -5x + 13
y - 7 = 5(x - 4)
(3) 3
You do NOT need to type all these into a graphing calculator (although you could, once you rewrote them in "y=" form).
Look at the first equation, 5x + y = 13. Substitute your x and y values.
5(2) + 3 = 13. True. 5(4) - 7 = 13. True. This is the equation of the line in Standard form.
Subtract 5x from both sides and you get y = -5x + 13, which is the equation in Slope-Intercept form, as well as the third equation.
The second equation y + 7 = -5(x - 4) is the equation in Point-Slope form, y - y0 = -5(x - x0).
The fourth equation has a slope of 5, instead of -5, and so it's incorrect.
21. The Ebola virus has an infection rate of 11% per day as compared to
the SARS virus, which has a rate of 4% per day.
If there were one case of Ebola and 30 cases of SARS initially reported to authorities and cases are reported each day, which statement is true?
(3) At day 10 there are more SARS cases, but at day 53 there are
more Ebola cases.
In case you were wondering were math gets used in the real world, in life-and-death instances, here you go.
Let's call Ebola, e(x), and SARS, s(x).
Then e(x) = 1(1.11)x and s(x) = 30(1.04)x
By day 53, Ebola will overtake SARS.
22. The results of a linear regression are shown below.
y = ax + b
a = -1.15785
b = 139.3171772
r = -0.896557832
r22 = 0.8038159461
Which phrase best describes the relationship between x and y?
(1) strong negative correlation. Only the r is important here. A number close to 1 indicates a strong positive correlation, and a number close to -1 indicates a strong negative correlation.
23. Abigail’s and Gina’s ages are consecutive integers. Abigail is younger than Gina and Gina’s age is represented by x. If the difference of the square of Gina’s age and eight times Abigail’s age is 17, which equation could be used to find Gina’s age?
(4) x2 - 8(x - 1) = 17.
Gina's age is x. So the square of Gina's age is x2. Abigail's age is (x - 1), so eight times Abigail's age is 8(x - 1). The difference between them is 17, so x2 - 8(x - 1) = 17.
Anything with (x + 1) can be immediately eliminated. Note that (1) would work if Abigail's age had been designated as x.
24. Which system of equations does not have the same solution as the
system below?
-6x - 5y = -16
(1)
(4) 40x + 30y = 100 and 36x + 30y = -96
The terms in the first equation were multiplied by 10. The terms in the second equation were multiplied by -6, except for the last term, which was multiplied by positive 6. Had the second equation ended is 96 instead of -96, then the systems would have had the same solution.
End of Part I. How did you do?

What's wrong with being square anyway? Is it worse than being rectangular or hexagonal?
Come back often for more funny math and geeky comics.


Numbers don't lie, but they can still be mean.
Come back often for more funny math and geeky comics.


Now, if we're going to talk about limits . . . best not to, actually.
Come back often for more funny math and geeky comics.


Open circles are the batteries of the number line.
And now that I've typed that, I realized I totally missed out on this joke's potential.
Come back often for more funny math and geeky comics.

Would potential work be ''U mad''?
Come back often for more funny math and geeky comics.


My pumpkin joke is running a little latte.
Come back often for more funny math and geeky comics.


With apologies to Pat Sajak. I don't want to know what happened to Vanna White.
Come back often for more funny math and geeky comics.


