More Algebra 2 problems.
January 2020, Part I
All Questions in Part I are worth 2 credits. No work need be shown. No partial credit.
1. The expression (81x8y6)1/4 is equivalent to
(1) 3x2y3/2
(2) 3x4y2
(3) 9x2y3/2
(4) 9x4y2
Answer: 1) 3x2y3/2
The fourth root (as seen in the picture) is the same as the 1/4 power (which I had to type).
The fourth root of 81 is 3. (The square root of 81 is 9. The square root of 9 is 3.)
The rule for exponents is to multiply the exponents: 8 * 1/4 = 2, 6 * 1/4 = 6/4 = 3/2.
2. Chet has $1200 invested in a bank account modeled by the function
P(n) = 1200(1.002)n, where P(n) is the value of his account, in dollars,
after n months. Chet’s debt is modeled by the function Q(n) = 100n,
where Q(n) is the value of debt, in dollars, after n months.
After n months, which function represents Chet’s net worth, R(n)?
(1) R(n) = 1200(1.002)n + 100n
(2) R(n) = 1200(1.002)12n + 100n
(3) R(n) = 1200(1.002)n - 100n
(4) R(n) = 1200(1.002)12n - 100n
Answer: 3) R(n) = 1200(1.002)n - 100n
Net worth is the amount of his savings minus his debt, so the first two choices are incorrect.
Everything in the problem is in terms of months, so there is no need to multiply the exponent by 12, which would convert n years into months.
3. Emmeline is working on one side of a polynomial identity proof used to form Pythagorean triples. Her work is shown below:
Step 1: 25x2 + (5x2 - 5)2
Step 2: 25x2 + 25x2 + 25
Step 3: 50x2 + 25
Step 4: 75x2
What statement is true regarding Emmeline’s work?
(1) Emmeline’s work is entirely correct.
(2) There is a mistake in step 2, only.
(3) There are mistakes in step 2 and step 4.
(4) There is a mistake in step 4, only.
Answer: 3) There are mistakes in step 2 and step 4.
There are two mistakes, and both Algebra 1 kinds.
In Step 2, Emmeline didn't square the binomial correctly. There should be a -50x2 term.
In Step 4, she combined two terms which are not alike.
4. Susan won $2,000 and invested it into an account with an annual
interest rate of 3.2%. If her investment were compounded monthly,
which expression best represents the value of her investment after
t years?
(1) 2000(1.003)12t
(2) 2000(1.032)t/12
(3) 2064t/12
(4) (2000(1.032)t)/12
Answer: 1) 2000(1.003)12t
The interest rate is given annually, but it is compounded monthly.
So instead of 2000(1.032)t, we need to do 2000(1.0321/12)12.
That is, we need to find the monthly interest rate by taking the 1/12 power, but then we need to multiply the number of years by 12 to get the number of months the account will be compounded.
1.0321/12 is approximately 1.003.
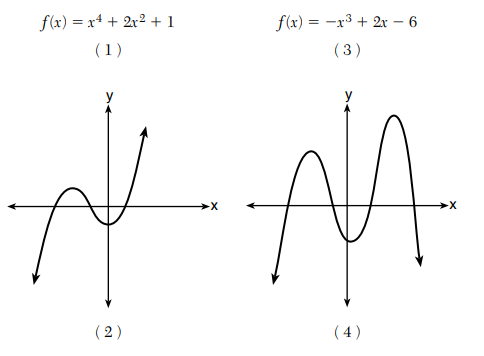
5.Consider the end behavior description below.
Which function satisfies the given conditions?
Answer: 3) f(x) = -x3 + 2x - 6
The conditions state, as x increases to infiinity, f(x) decreases, and as x decreases to negative infinity, f(x) increases.
Graph (2) has the opposite behavior.
Graph (4) goes to negative infinity on both ends.
Function (1) has positive exponents only and will increase on both sides.
Function (3) is a negative cubic function, so it will start high and end low.
Comments and questions welcome.
More Algebra 2 problems.



















No comments:
Post a Comment