August 2019 Geometry Regents Parts 3 & 4

The following are some of the multiple questions from the August 2019 New York State Geometry Regents exam.

August 2019 Geometry, Part III

Each correct answer is worth up to 4 credits. Partial credit is available. Work must be shown. Correct answers without work receive only 1 point.

32. Triangle ABC is shown below. Using a compass and straightedge, construct the dilation of Triangle ABC centered at B with a scale factor of 2. [Leave all construction marks.]

Is the image of triangle ABC similar to the original triangle? Explain why.

Answer:
Starting at point B, open the compass to Point A. Then from point A, make an arc. Use the straightedge to extend BA to the new arc. This line will have twice the length of BA.
Repeat the process for BC.
Finally, using the straightedge, complete the triangle from the endpoints of the two new line segments you constructed.

The image is similar to the original triangle because a dilation preserves the shape of the object. Therefore, the angles are the same size and by the AA Theorem, the two triangles are similar.

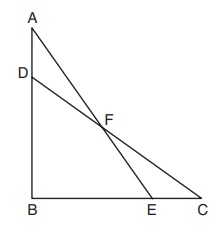
33. In the diagram below, triangle ABE = triangle CBD.

Prove: triangle AFD = triangle CFE

Answer:
You need to prove that those two tiny triangles are similar.
You can see that Angles A and C are equal from the original triangles. And angles AFD and CFE are vertical angles. You need to have one pair of congruent sides.

You don't know that AD = CE directly, but you do know that AB = CB and DB = EB because of the congruency of the larger triangles. Therefore if you subtract the smaller segment from the larger one, you get the sides that we need to be congruent.

Your proof would go something like this:

Statement	Reason
1. Triangle ABE = Triangle CBD	1. Given
2. Angle A = Angle C	2. CPCTC
3. Angle AFD = Angle CFE	3. Vertical angles are congruent.
4. AB = CB; DB = EB	4. CPCTC
5. AD = CE	5. Subtraction Postulate
6. triangle AFD = triangle CFE/td>	6. AAS

34. A cargo trailer, pictured below, can be modeled by a rectangular prism and a triangular prism. Inside the trailer, the rectangular prism measures 6 feet wide and 10 feet long. The walls that form the triangular prism each measure 4 feet wide inside the trailer. The diagram below is of the floor, showing the inside measurements of the trailer.

If the inside height of the trailer is 6.5 feet, what is the total volume of the inside of the trailer, to the nearest cubic foot?

Answer:
Volume = Area of the Base times the Height.
The base is shaped like a pentagon, which, in this case, can be broken into a rectangle and a triangle. We have the base of the triangle, 6 feet; however, we need to solve for its height (lower case h). We can use the Pythagorean Theorem for this.

3² + x² = 4²
9 + x² = 16
x² = 7
x = SQRT(7) = 2.65 (approximately)
Area of the base = (6)(10) + (1/2)(6)(2.65) = 67.95
Volume = Area * height = 67.95 * 6.5 = 441.675 = 442 cubic feet

Part IV

A correct answer is worth up to 6 credits. Partial credit is available.

35. The coordinates of the vertices of Triangle ABC are A(1,2), B(-5,3), and C(-6,-3).

Prove that Triangle ABC is isosceles
[The use of the set of axes on the next page is optional.]

State the coordinates of point D such that quadrilateral ABCD is a square.
Prove that your quadrilateral ABCD is a square.
[The use of the set of axes below is optional.]

Answer:
Two separate questions.
First, to prove that ABC is isosceles, you will have to show that two of the sides have the same length.
It can be assumed from the second part of the question even before we start that it will be a right triangle, because that is the only way that you will be able to add one more point and have a square. Furthermore, AB and BC would have to be the congruent sides.

The second and third parts are really the same question. Once you have the square, you have to prove that it is a square. This is more rigorous than just an "explanation" or "justification". However, by this point you have already shown that two consecutive sides are congruent, so all you have to do is show that the sides are parallel, making it both a parallelogram and a rhombus, and that there is at least one right angle, which makes it a square.

First Part:
Length of AB = SQRT( (-5 - 1)² + (3 - 2)² ) = SQRT(37)
Length of BC = SQRT( (-6 - -5)² + (-3 - 3)² ) = SQRT(37)
AB = BC, so triangle ABC is isosceles.
(No reason to check the length of AC.

Second Part:
To get from point A to B, you have to go down 6 left and up 1. (This can be seen if you graph it, or if you worked out the math above.) CD would have to have the same slope, but to get from C to D, you would have to go 6 right and down 1. So D would have to be (-6 + 6, -3 - 1) or D(0, -4).

Third part:
The slope of AB = -1/6. The slope of CD = -1/6
The slope of BC = (-3 -3)/(-6 - -5) = -6/-1 = 6
The slope of DA = (-4 - 2)/(0 - 1) = -6 / -1 = 6

AB || CD, AD || BC because they have the same slopes.
AB is perpendicular to BC because their slopes are inverse reciprocals (have a product of -1).
So Angle B is a right angle.

A quadrilateral with opposite sides parallel, with consecutive sides equal and a right angle must be a square.

End of Exam

How did you do?
Comments and corrections welcome. (I get many of the latter!)