Below are the questions with answers and explanations for Part 1 the Geometry (Common Core) Regents exam for January 2016. Part II questions appeared in a another post.
Part I
1. William is drawing pictures of cross sections of the right circular cone below. (image omitted)
Which drawing can not be a cross section of a cone?
(1) the square. You can make a slice through that cone and get an oval (or circle), a semicircle with a diameter on the bottom or even triangle if you split it vertically. You can't get a square.
2. An equation of a line perpendicular to the line represented by the equation y = -(1/2)x - 5 and passing through (6, -4) is
(4) y = 2x - 16. A line perpendicular to a line with a slope of -1/2 would have a slope of 2, so (1) and (2) are out. If you plug in 6 for x, -4 = 2(6) + b, b = -16.
3. In parallelogram QRST shown below, diagonal TR is drawn, U and V are points on TS and QR, respectively, and UV intersects TR at W.
If m<S = 60°, m<SRT = 83°, and m<TWU = 35°, what is m< WVQ?
(3) 72°. Look at quadrilateral QTWV, which has 360°. Angle Q = S = 60. Angle QTV = SRT = 83. Angle TWV = 180 - TWU = 180 - 35 = 145. 60 + 83 + 145 = 288. 360 = 288 = 72°.
4. A fish tank in the shape of a rectangular prism has dimensions of 14 inches, 16 inches, and 10 inches. The tank contains 1680 cubic inches of water. What percent of the fish tank is empty?
(2) 25. The volume of the tank is 14 * 16 * 10 = 2240. 2240 - 1680 = 560 gallons empty. 560 / 2240 = .25 = 25%
5. Which transformation would result in the perimeter of a triangle being different from the perimeter of its image?
(3) (x,y)--> (4x,4y). A dilation would change the distance between the vertices, and therefore the perimeter. Reflections and translations do not affect the size, so the image would have the same perimeter.
6. In the diagram below, FE bisects AC at B, and GE bisects BD at C.
Which statement is always true?
(1) AB = DC. Because of bisecting AB = BC and BC = CD. Therefore, AB = CD. We have no information about where points F or G are, so you cannot make any assumptions about those lines being bisected or the segments being equal.
7. As shown in the diagram below, a regular pyramid has a square base
whose side measures 6 inches. (image omitted)
If the altitude of the pyramid measures 12 inches, its volume, in cubic inches, is
(2) 144. The Volume is (1/3)(Area of the Base)(height) = (1/3)(6 * 6)(12) = (12)(12) = 144.
8. Triangle ABC and triangle DEF are graphed on the set of axes below.
Which sequence of transformations maps triangle ABC onto
triangle DEF?
(1) a reflection over the x-axis followed by a reflection over the y-axis. It is also a 180 degree rotation about the origin, but it would NOT be followed by a reflection in y = x.
9. In triangle ABC, the complement of <B is <A. Which statement is always true?
(4) sin <A =cos <B. The sine of one complementary angle is the cosine of the other in a right triangle. The side opposite angle A will be adjacent to angle B.
10. A line that passes through the points whose coordinates are (1,1) and (5,7) is dilated by a scale factor of 3 and centered at the origin. The image of the line
(2) is parallel to the original line. As long as the line does not go through the origin, its dilation will be a parallel line (having the same slope). If the line went through the origin, it would be the same line. The slope of the line is 6/4 = 3/2. The line y = 3/2x does not go through (1, 1), so the line being dilated does not go through the origin.
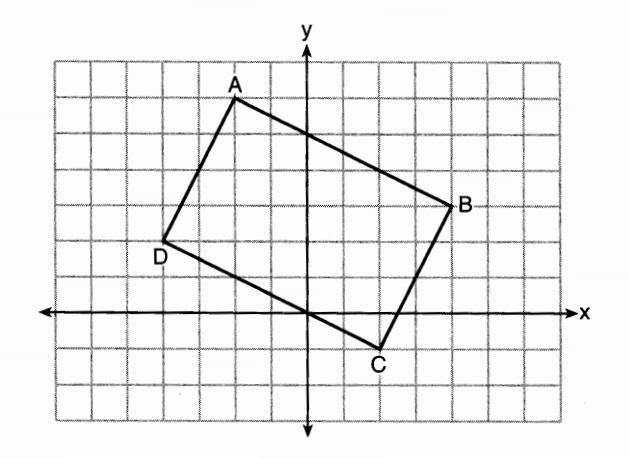
11. Quadrilateral ABCD is graphed on the set of axes below.
When ABCD is rotated 90° in a counterclockwise direction about
the origin, its image is quadrilateral A' B 'C 'D'. Is distance preserved
under this rotation, and which coordinates are correct for the given
vertex?
(4) yes and B'(-3,4) . Yes, distance is preserved, (1) and (2) are eliminated. A(-2, 6) will move to A'(-6, -2). Choice (3) would have been correct for a clockwise rotation.
12. In the diagram below of circle 0, the area of the shaded sector LOM
is 2(pi) cm2.
If the length of NL is 6 cm, what is m<N?
(3) 40°. The diameter is 6 cm, so the radius is 3 cm. That makes the Area of the entire circle = (pi)(3)2 = 9pi.
if the shaded sector is 2pi, then that sector and that arc is 2/9 of the circle, which is 2/9(360) = 80 degrees. Angle N is an inscribed angle that intercepts arc LM, so it is half of 80 degrees, or 40 degrees.
13. In the diagram below, triangle ABC ~ triangle DEF.
If AB = 6 and AC = 8, which statement will justify similarity by SAS?
(1) DE = 9, DF = 12, and <A = <D. Angles A and D are the included angles, so (3) and (4) are eliminated. 6/8 = .75 and 9/12 = .75, so they are proportional.
14. The diameter of a basketball is approximately 9.5 inches and the diameter of a tennis ball is approximately 2.5 inches. The volume of the basketball is about how many times greater than the volume of the tennis ball?
(3) 55. The radius of the basketball is 4.75. The radius of the tennis ball is 1.25. Volume requires cubing the radii. Divide (4.753 / 1.253) = 54.872, which is approximately 55.
15. The endpoints of one side of a regular pentagon are (-1,4) and (2,3). What is the perimeter of the pentagon?
(2) 5*SQRT(10). Using the Distance formula (or the Pythagorean Theorem), we can find the length of the segment joining those two endpoints to be SQRT(32 + 12), which is SQRT(10). Since there are five sides to a pentagon, the perimeter is 5*Sqrt(10). [5 radical 10]
16. In the diagram of right triangle ABC shown below, AB = 14 and AC= 9. (image omitted)
What is the measure of <A, to the nearest degree?
(3) 50. AC is the adjacent side and AB is the hypotenuse, so cos A = 9/14. That means <A = cos-1(9/14) = 49.99... degrees.
17. What are the coordinates of the center and length of the radius of the circle whose equation is x2 + 6x + y2 - 4y = 23?
(4) (-3,2) and 6 You need to complete the squares to find the equation for the circle. (I could make a comic out of that sentence.)
Half of +6 is +3, and half of -4 is -2, but you have to flip the signs to find (h, k). Remember: (x - h)2 + (y - k)2.
So the center is at (-3, 2) and you eliminate (1) and (2).
To complete the square you need to add (3)2 add (-2)2 to both sides of the equations. That adds 9 + 4 to 23, giving 36, which is r2. So the radius is 6 (not 36).
18. The coordinates of the vertices of triangle RST are R(-2, -3), S(8,2), and T(4,5). Which type of triangle is triangle RST?
(1) right. Eliminate (4) equiangular, because equiangular/equilateral triangles are always acute, and you can't have two correct answers.
If the triangle is right, then two of the sides will have perpendicular slopes -- that is, they will be negative reciprocals. If that is not true, then you have to find the lengths of the three sides to determine if the triangle is acute or obtuse.
Slope of RS = (2 - -3)/(8 - -2) = 5/10 = 1/2. Slope of ST = (5 - 2)/(4 - 8) = 3/(-4) = -(3/4). Slope of TR = (-3 - 5)/(-2 - 4) = -8/-6 = 4/3. ST is perpendicular to TR because (-3/4)(4/3) = -1. It is a right triangle.
19. Molly wishes to make a lawn ornament in the form of a solid sphere. The clay being used to make the sphere weighs .075 pound per cubic inch. If the sphere's radius is 4 inches, what is the weight of the sphere, to the nearest pound?
(2) 20. Multiply the Volume of the sphere by .075, so .075(4/3)(pi)(4)3 = 20.1..., which is about 20.
20. The ratio of similarity of triangle BOY to triangle GRL is 1:2. If BO = x + 3 and GR = 3x - 1, then the length of GR is
(4) 20. Because GR is twice as big as BO, start with 2(x + 3) = 3x - 1,
So 2x + 6 = 3x - 1
and 7 = x. (note that this is choice (2).)
The length of GR is 3(7) - 1 = 20.
21. In the diagram below, DC, AC, DOB, CB, and AB are chords of circle O, FDE is tangent at point D, and radius AO is drawn. Sam decides to apply this theorem to the diagram: "An angle inscribed in a semi-circle is a right angle."
Which angle is Sam referring to?
(3) <DCB. DOB is a diameter of the triangle and arc DAB is a semi-circle. Angle DCB is an inscribed angle that intercepts the semi-circle. Since it is half the measure of the 180 degrees, it must be 90 degrees, making it a right angle.
22. In the diagram below, CD is the altitude drawn to the hypotenuse AB
of right triangle ABC. (image omitted)
Which lengths would not produce an altitude that measures 6*SQRT(2)?
(2) AD = 3 and AB = 24 Square (6*SQRT(2)) and you get 36 * 2 = 72 as the altitude. The product of AD and DB must be 72 for the altitude to be 6*SQRT(2). Read the choices carefully. Two of the choices give you AB, not DB. You need to subtract AD from AB to get DB. While 3 * 24 equals 72, you are supposed to be multiplying 3 * 21, which is only 63.
23. A designer needs to create perfectly circular necklaces. The necklaces each need to have a radius of 10 cm. What is the largest number of necklaces that can be made from 1000 cm of wire?
(1) 15. If the radius is 10 cm, then the length of the wire to produce one necklace, (2)(10)(pi), is approximately 62.83 cm. Divide 1000/62.83 and you get 15.9. However, you cannot round up because you don't have enough wire to finish the 16th necklace.
24. In triangle SCU shown below, points T and O are on SU and CU, respectively. Segment OT is drawn so that <C = <OTU.
If TU = 4, OU = 5, and OC = 7, what is the length of ST?
(3) 11. Triangles OUT and CUS are similar, and the sides are proportional, but make sure you set up the proportion correctly. OT is NOT parallel to CS. The correct proportion is 4/(7 + 5) = 5/(4 + x), so 16 + 4x = 60.
4x = 44, x = 11.
END OF PART 1.
I also write Fiction!Check out In A Flash 2020, by Christopher J. Burke for 20 great flash fiction stories, perfectly sized for your train rides. Available in softcover or ebook at Amazon. If you enjoy it, please consider leaving a rating or review on Amazon or on Good Reads. Thank you. |
 |



















10 comments:
I don't get #22
I don't understand 22
In 22 where do you get 21 from???
AD X DB = (CD)^2
Choices 2 and 4 do NOT say DB, they say AB. AB is the length of AD + DB.
To find the length of DB you need to subtract DB = AB - AD.
So if AB = 24 and AD = 3, then DB = 21
Hope this helps
I wrote more about question 22 here:
http://mrburkemath.blogspot.com/2016/06/daily-regents-right-triangle-altitude.html
Thank you so much!!!
I dont under stand the proportion you set up for question #24, wouldent it be 4/5 = x + 4/12?
When you set up the proportion with similar triangles, you need to compare the corresponding sides.
If you notice from the picture, the bases of the two triangles are NOT parallel. This is because the smaller triangle is basically a flipped over version of the bigger one.
You can't trust the image (because it doesn't have to be drawn to scale), but if you read the problem, you can see which angles are congruent. The opposite sides are the corresponding sides.
Hello can I get help for number 24 I don't understand this question you said it's flipped then shouldn't ou become 4 and tu 5
And also I tried this problem and I set up like this
X/X+5 = 7/11
It mean a lot if you help me I got regents tommrow
Post a Comment