The following are questions from the recent August 2020 New York State Common Core Geometry Regents exam.
A correct answer is worth up to 6 credits. Partial credit can be earned. Work must be shown or explained.
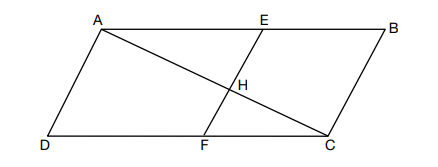
35.
Given: Quadrilateral ABCD, AC and EF intersect at H, EF || AD, EF || BC, and AD ≅ BC.
Prove: (EH)(CH) = (FH)(AH)
Answer:
August 2022 Geometry, Part IV
This is an unusual proof, in my opinion. Usually, the final line is some theory of congruence, like SAS or CPCTC, etc. This one shows two products. However, it's really the cross-products of a proportion. Looking at the figure, the proportion seems to be created by the corresponding sides of similar triangles. Once you have that proportion, the final line comes from the product of the means and the extremes being equal.
| Statement | Reason |
| 1. Quadrilateral ABCD, AC and EF intersect at H, EF || AD, EF || BC, and AD ≅ BC. | Given |
| 2. AD || BC | If two lines are parallel to a given line then they are parallel to each other. (Transitive property) |
| 3. ABCD is a parallelogram | If the opposite sides of a quadrilateral are parallel then the quadrilateral is a parallelogram. |
| 4. AB || CD | Opposite sides of a parallelogram are parallel. |
| 5. ∠BAC ≅ ∠DCA | Alternate interior angles are congruent. |
| 6. ∠AHE ≅ ∠CHF | Vertical angles are congrunt |
| 7. △AHE ~ △CHF | AA Postulate |
| 8. EH/FH = AH/CH | If two triangles are similar, then their corresponding sides are proportional. |
| 9. (EH)(CH) = (FH)(AH) | The product of the means = the product of the extremes. |
End of Part Exam
How did you do?
Questions, comments and corrections welcome.
I also write Fiction!Check out In A Flash 2020, by Christopher J. Burke for 20 great flash fiction stories, perfectly sized for your train rides. Available in softcover or ebook at Amazon. If you enjoy it, please consider leaving a rating or review on Amazon or on Good Reads. Thank you. |
 |
















No comments:
Post a Comment