Now that I'm caught up with the current New York State Regents exams, I'm revisiting some older ones.
More Regents problems.
Algebra 2/Trigonometry Regents, January 2011
Part I: Each correct answer will receive 2 credits.
1. Which graph does not represent a function?
Answer: 4) [SEE IMAGE]
The last choice fails the vertical-line test, so it is not a function.
No x value can have multiple y values in a function.
2. The roots of the equation x2 − 10 x + 25 = 0 are
1) imaginary
2) real and irrational
3) real, rational, and equal
4) real, rational, and unequal
Answer: 3) real, rational, and equal
If you graph the equation in your graphing calculator, you will see that it touches the x-axis at its vertex. That eliminates Choices (1) and (4).
If you check the Table of Values, you will see that the vertex is x = 5. You could also have used x = -b/(2a) to find that.
So the roots are rational. And they are equal.
If you factored, you would have had y = (x - 5)(x - 5), which tells you x = 5 is the only root.
3. Which values of x are solutions of the equation x3 + x2 − 2x = 0?
1) 0, 1, 2
2) 0, 1, -2
3) 0, -1, 2
4) 0, -1, -2
Answer: 2) 0, 1, -2
Obviously x = 0 is a solution, and it's in all four choices. You can factor or you can use substitution to find the other two. Since the final sign is negative, you know it has to be (2) or (3), so if you are substituting, start with those.
x3 + x2 − 2x = 0
x(x2 + x − 2 = 0
x(x + 2)(x - 1) = 0
x = 0 or x = -2 or x = 1
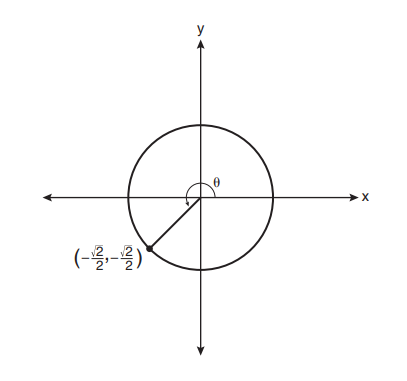
4. In the diagram below of a unit circle, the ordered pair (−√2/2, −√2/2) represents the point where the terminal side of θ intersects the unit circle.
What is m∠θ?
1) 45
2) 135
3) 225
4) 240
Answer: 3) 225
First, the point is in Quadrant III, so the measure must be 1800 < θ < 270. This eliminates Choices (1) and (2).
Second, you should know that (√2/2, √2/2) represents 45 degrees. Add 180 to that and you have 225, which is Choice (3).
5. What is the fifteenth term of the sequence 5, −10, 20, −40, 80, . . . ?
1) −163,840
2) −81,920
3) 81,920
4) 327,680
Answer: 3) 81,920
Notice that the odd terms are positive, so the fifteenth term (15th, not 50th) must be positive. Eliminate Choices (1) and (2).
The common ratio is the sequence is -10/5 = -2, 20/-10 = -2, etc. (You will notice that it does NOT have a common difference, so it is not arithmetic.)
The fifteenth term is (5)(-2)14 = 81,920.
More to come. Comments and questions welcome.
More Regents problems.
I also write Fiction!You can now preorder Devilish And Divine, edited by John L. French and Danielle Ackley-McPhail, which contains (among many, many others) three stories by me, Christopher J. Burke about those above us and from down below. Preorder the softcover or ebook at Amazon. Also, check out In A Flash 2020, by Christopher J. Burke for 20 great flash fiction stories, perfectly sized for your train rides. Available in softcover or ebook at Amazon. If you enjoy it, please consider leaving a rating or review on Amazon or on Good Reads. |
 |
 |