The State of Texas Assessments of Academic Readiness (STAAR) exam, administered MAY 2018.
More STAAR problems.
Administered May 2018
Read each question carefully. For a multiple-choice question, determine the
best answer to the question from the four answer choices provided. For a
griddable question, determine the best answer to the question.
36. Which expression is equivalent to (h2 + 9h − 1)(−4h + 3)?
F −4h3 − 33h2 + 31h − 3
G 4h3 + 39h2 − 23h − 3
H −4h3 − 39h2 + 23h + 3
J 4h3 + 33h2 − 31h + 3
Answer: F −4h3 − 33h2 + 31h − 3
It should be obvious that the leading term will be the product of h2 and -4h, which will be -4h3. That eliminates G and J.
Likewise, the final term is the product of (-1) and (3), which is -3, which eliminates H.
If you needed to work it out, do the following:
(h2 + 9h − 1)(−4h + 3)
-4h3 + 3h2 - 36h2 + 27h + 4h - 3
-4h3 - 33h2 + 31h - 3
37.
There are 15 plates in a kitchen cabinet. The diameter of each plate is either 7 inches or
12 inches. The diameter of all 15 plates combined is 140 inches.
Which system of equations can be used to find the number of 7-inch plates, x, and the
number of 12-inch plates, y, that are in the cabinet?
A x + y = 140 ; 12x + 7y = 15
B 7x + 12y = 140 ; 7x + 12y = 15
C x + y = 15 ; 7x + 12y = 140
D x + y = 15 ; 12x + 7y = 140
Answer: C x + y = 15 ; 7x + 12y = 140
The total number of plates is 15, so x + y = 15. Eliminate A and B.
The variable x is defined to be the 7-inch plates, so the total number of inches in diamter is 7x, not 12x. Likewise, the number of 12-inch plates is y, so we need 12y.
If you were solving this problem on your own, and the variables had not been pre-defined for you, then there would be no difference in using either C or D to solve the problem, as long as you knew which varaible stood for which object.
Choice A is backward with its 140 and 15 -- 140 dishes have a combined diameter of 15 inches? It must be a miniatures collection, or toys in a tiny doll house. Choice B has a pair of parallel lines, which has no solution.
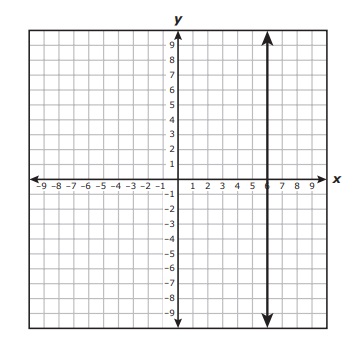
38. The graph of quadratic function f is shown on the grid.
Which of these best represents the domain of f ?
F −3 ≤ x ≤ 2
G All real numbers
H y ≥ 5.5
J All real numbers less than −3 or greater than 2
Answer: G All real numbers
Domain is the valid x values that can be input to the function. There are no numbers for which this quadratic is undefined. Just because only −3 ≤ x ≤ 2 is shown doesn't mean that that is the entirety of the graph. (Note the arrows at the ends of the line.)
Choice H would be correct for the Range. When you see something like this, always go back and reread the question. Make sure it said what you thought it said. (You'd be surprised at the number of times a person can misread something and instead read what they expected to see instead of what was there.)
39.What is the equation in slope-intercept form of the line that passes through the point (2, −2)
and is perpendicular to the line represented by y = 2/5 x + 2?
A y = 5/2 x − 7
B y = 5/2 x + 7
C y = −5/2 x − 3
D y = −5/2 x + 3
Answer: D y = −5/2 x + 3
The slope of a line perpendicular to another line must be the inverse reciprocal of the slope of the original line. That is, the two slopes will have a product of -1.
The inverse reciprocal of 2/5 is -5/2. Eliminate A and B.
Substitue x = 2 into the other equations, and see which gives you -2.
y = -5/2 (2) - 3 = -5 - 3 = -8
y = -5/2 (2) + 3 = -5 + 3 = -2.
To work it out, if there weren't any choices, use slope-intercept form:
y - (-2) = -5/2 (x - 2)
y + 2 = -5/2 x + 5
y = -5/2 x + 3
40. Which graph best represents f(x) = 2(5)2?
Answer: F
When x = 0, 5x = 50 = 1, and 2(1) = 2.
When x = 1, 5x = 51 = 5, and 2(5) = 10.
The only graph with (0, 2) [approximately] and (1, 10) is graph F.
Choice J looks like f(x) = 5(2)x.
Choice H looks like f(x) = 10(2)x.
Choice G looks like f(x) = 5x.
More to come. Comments and questions welcome.
More STAAR problems.