Look before you Leap! (The A.P. frowns on fun.)
Combine with light sabers for an extra cinematic feel.
Apparently, the last time I did a Leap Day comic was eight years ago when I was really just getting started.
Come back often for more funny math and geeky comics.
Monday, February 29, 2016
Leap Day!
Friday, February 26, 2016
(x, why?) Mini: Cheers!
Raise a glass and talk charts and graphs!
I hate when my "quickie" comics take longer than my regular ones. I realized halfway through that I probably should have expanded it beyond the usual "mini" borders. Too late.
I don't usually go 9 days without an update. It's not for a lack of ideas, but a lack of (Time AND Energy).
Come back often for more funny math and geeky comics.
Sunday, February 21, 2016
January 2016 Geometry (not Common Core) Regents, Part 2
Below are the questions with answers and explanations for Part 2 of the New York State Geometry Regents (not Common Core) exam for January 2016. Part I questions appeared in here.
Part II
29. The sides of a triangle measure 7, 4, and 9. If the longest side of a similar triangle measures 36, determine and state the length of the shortest side of this triangle.
The triangles are similar so the sides are proportional. Write a proportion:
4 / 9 = x / 36
9x = (4)(36)
9x = 144
x = 16. The shortest side of the triangle is 16.
Or, you can state that 36/9 = 4. The Scale factor is 4. Therefore the shortest side is 4 * 4 = 16.
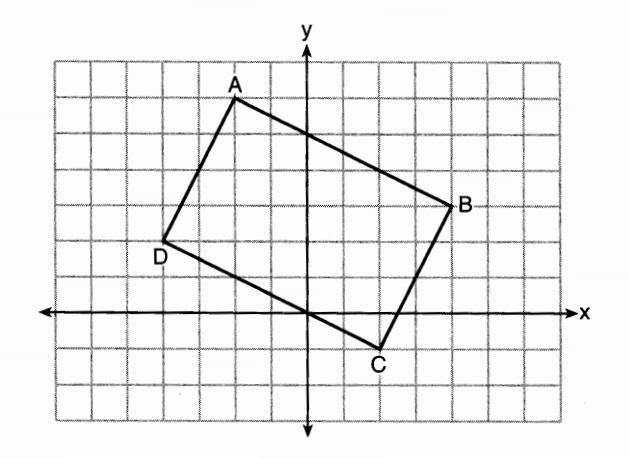
30. Triangle ABC has coordinates A(6, -4), B(0,2), and C(6,2). On the set of axes below, graph and label triangle A'B'C', the image of triangle ABC after a dilation of 1/2.
Graph the points A'(3, -2), B'(0, 1), C'(3, 1) and draw the lines. Don't forget to label the points.
31. In parallelogram RSTU, m<R = 5x - 2 and m<S = 3x + 10. Determine and state the value of x.
R and S are consecutive angles in a parallelogram, so they are supplementary.
Therefore, 5x - 2 + 3x + 10 = 180
8x + 8 = 180
8x = 172
x = 22
If you set them equal to each other, that would be a conceptual error. You would have lost one point for that. You could get one point if your answer is consistent with the error.
32. Determine and state the length of a line segment whose endpoints are (6,4) and (-9, -4).
Use the Distance Formula, or Pythagorean Theorem.
Sqrt ( (-9-6)2 + (-4-4)2) =
Sqrt ( (-15)2 + (-8)2) =
Sqrt ( 225 + 64 ) =
sqrt ( 289 ) = 17.
If you figured that the change in x was 15 and change in y was 8, you could have used Pythagroean Theorem to get 17, also.
33. The base of a right pentagonal prism has an area of 20 square inches. If the prism has an altitude of 8 inches, determine and state the volume of the prism, in cubic inches.
V = Area of Base * Height = 20 * 8 = 160.
That seems like the easiest two points you'll get. I reread it three times thinking I missed something.
34. Using a compass and a straightedge, construct the bisector of <CDE. [Leave all construction marks.]
Construction coming soon. They aren't easy to do on the computer.
Steps: 1. From D make an arc that intersects DE and DC.
2. From the point you made on ED, make an arc inside the pentagon.
3. From the point you made on DC, make another arc the same size as the last one so that they overlap.
4. With the straightedge, draw the angle bisector from point D to the point where the two arcs intersected.
Thursday, February 18, 2016
January 2016 Geometry (not Common Core) Regents, Part 1
Below are the questions with answers and explanations for Part 1 of the New York State Geometry Regents (not Common Core) exam for January 2016.
Part I
1. What is the equation of a circle with its center at (5,-2) and a radius of 3?
(2) (x - 5)2 + (y + 2)2 = 9. Flip the signs on (h, k) and square the radius.
2. In the diagram below, <ABC is inscribed in circle 0.
The ratio of the measure of <ABC to the measure of arc AC is
(2) 1:2. The ratio of the inscribed angle to the arc it intercepts is 1:2. In other words, the arc is twice the size of the inscribed angle.
3. In the diagram below of rectangle RSTU, diagonals RT and SU
intersect at 0.
If RT = 6x + 4 and SO = 7x - 6, what is the length of US?
(3) 16. The diagonals of a rectangle are congruent so RT = US. The diagonals of a rectangle also bisect each other, so the length of UO = SO, and US = 2(SO). So US = 14x - 12.
8x = 16
x = 2
US = 14(2) - 12 = 28 - 12 = 16
4. How many points are 3 units from the origin and also equidistant from both the x-axis and y-axis?
(4) 4. Three units away from the origin is a circle. Equidistant from the x-axis and y-axis are two diagonal lines (y = x and y = -x). The circle intersects each line twice. Four points.
5. The converse of the statement "If a triangle has one right angle, the triangle has two acute angles" is
(1) If a triangle has two acute angles, the triangle has one right angle. Note that the converse does not have the same Truth value as the statement.
6. The surface area of a sphere is 2304(pi) square inches. The length of a radius of the sphere, in inches, is
(2) 24. The formula for the Surface Area of a sphere is 4(pi)r2 = 2304(pi). Dividing by 4 gives you 576. Take the square root, and the radius is 24.
7. As shown in the diagram below of triangle ABC, BC is extended through D,
m<A = 70, and m<ACD = 115.
Which statement is true?
(4) AC < AB. Angle ACB is 65o and angle B is 45o. So AC < AB < BC
8. In trapezoid LMNO below, median PQ is drawn.
If LM = x + 7, ON = 3x + 11, and PQ = 25, what is the value of x?
(3) 8. The length of the median of a trapezoid is half the sum of the base heights. That is, it's is the average of the length of the two bases. So x + 7 + 3x + 11 = 25 * 2.
4x + 18 = 50
4x = 32
x = 8. The three lines would be 15, 25 and 35.
9. Points A and B are on line L. How many points are 3 units from line L and also equidistant from A and B?
(2) 2. Second Locus question. Equidistant from line L are two lines parallel to L. Equidistant to points A and B is the perpendicular bisector of AB, which will intersect each of the two parallel lines.
10. The lines whose equations are 2x + 3y = 4 and y = mx + 6 will be perpendicular when m is
(3) 3/2. The slope of the perpendicular line is the inverse reciprocal of the first line. Subtract 2x from both sides and divide by three, and the slope of the first line is -2/3. The inverse reciprocal is 3/2.
11. As shown in the diagram below, M, R, and T are midpoints of
the sides of triangle ABC.
If AB = 18, AC 14, and BC 10, what is the perimeter of quadrilateral ACRM?
(1) 35. MR is a midsegment, so it is parallel to AC and half of its size. AM is 9, AC is 14, CR is 5 and RM is 7. Add 9 + 14 + 5 + 7 = 35.
12. In the diagram below, ABC || DEFG. Transversal BHE and line segment HF are drawn.
If m<HFG = 130 and m<EHF = 70, what is m<ABE?
(3) 60. Angle HFG is an exterior angle to triangle EFH. Angles EHF and HEF are remote angles with a sum of 130 degrees. Angle EHF = 70, so HEF = 60. Angle ABE and HEF are alternate interior angles, so they are congruent.
13. The graphs of the lines represented by the equations y = (1/3)x + 7 and y = -(1/3)x - 2 are
(4) intersecting, but not perpendicular. Second question about the slopes of perpendicular lines. The product of (1/3) and (-1/3) is NOT -1, so they are not perpendicular.
14. Which graph represents a circle whose equation is (x + 3)2 + (y - 1)2 = 4?
(1). The circle with the center at (-3, 1) with a radius of 2. Second question about the equation of a circle.
15. In triangle ABC, m<CAB = 2x and m<ACB = x + 30. If AB is extended through point B to point D, m<CBD = 5x - 50. What is the value of x?
(3) 40. Make a diagram if it helps.
Angles CAB and ACB are remote angles to exterior angle CBD. So the sum of 2x + x + 30 = 5x - 50.
3x + 30 = 5x - 50
80 = 2x
40 = x.
The angles of ABC are 80, 70 and 30. The exterior angle is 150.
16. In circle O shown below, chord AB and diameter CD are parallel,
and chords AD and BC intersect at point E.
Which statement is false
(2) BE = CE. The two triangles, ABE and CDE, will be similar but not congruent, so point E is NOT the midpoint of BC. If you draw in AC and BD, you will have an isosceles trapezoid. The diagonals of an isosceles trapezoid do NOT bisect each other.
17. When the transformation T(2,-1) is performed on point A, its image is point A'(-3,4). What are the coordinates of A?
(2) (-5, 5). (-5 + 2 = -3, 5 - 1 = 4).
18. If the sum of the interior angles of a polygon is 1440°, then the polygon must be
(2) a decagon. I should go as far as to say that you should recognize the number if you did any of these problems, but I'll explain anyway. The formula is (n - 2) * 180 = 1440, so n - 2 = 8, n = 10. Ten sides is a decagon. If you didn't remember the formula, you could have started with a triangle and kept adding 180 degrees until you hit 1440.
19. In triangle ABC shown below, medians AD, BE, and CF intersect at
point R.
If CR = 24 and R F= 2x - 6, what is the value of x?
(1) 9. Medians meet at the centroid, and the distance from the angle to the centroid is twice the distance from the centroid to the midpoint of the opposite side.
CR is twice the size of RF, so 2x - 6 = 12. Then 2x = 18 and x = 9.
20. Which equation represents a line that passes through the point (-2,6) and is parallel to the line whose equation is 3x - 4y = 6?
(3) -3x + 4y = 30. Parallel lines have the same slope. The slope of each line is 3/4.
-3(-2) + 4(6) = 6 + 24 = 30. Check. (Note that choice (3) was the only possibility based on slope alone, but it's a good idea to check the point anyway. Just in case.)
21. The bases of a right prism are triangles in which triangle MNP = triangle RST. If MP = 9, MR = 18, and MN = 12, what is the length of NS?
(4) 18. I had to read that one twice to see if this was a trick question. But that depends on what you think is a trick question. If it is a prism, then the bases are parallel to each other. That makes MR, NS and PT are the same size, which is 12. If you set up ratios or tried the Pythagorean Theorem, you were incorrect.
22. Triangle ABC has the coordinates A(3,0), B(3,8), and C(6,6). If triangle ABC is reflected over the line y = x, which statement is true about the image of triangle ABC?
(1) One point remains fixed. If you reflect it over y = x, the point (6, 6) will remain at (6, 6) because it is on the line y = x. (e.g., 6 = 6) The size remains the same. The orientation changes. And the final statement, besides not being true, has nothing to do with the image or the reflection.
23. A right circular cone has a diameter of 10(sqrt(2)) and a height of 12. What is the volume of the cone in terms of pi?
(1) 200 pi. The volume is (1/3)(pi)r2h = (1/3)(pi)(5(sqrt(2))(12) = 200 pi.
Choice (2) is if you forgot the (1/3). Choices (3) and (4) if you forgot to halve the diameter before squaring.
24. Which statement is not always true when triangle ABC = triangle XYZ?
(2) CA = XY. If you didn't get this one correct, it might be because your teacher wasn't careful enough in examples. Or because you didn't pay attention the time they mentioned that when written properly, each letter, in order, should correspond. So A to X, B to Y, C to Z.
25. If two sides of a triangle have lengths of (1/4) and (1/5), which fraction can not be the length of the third side?
(4) 1/2. The third side cannot be bigger than 1/4 + 1/5 nor smaller than 1/4 - 1/5. One half is greater than 9/20. Also, 1/2 = 1/4 + 1/4 which is bigger than 1/4 + 1/5.
26. In the diagram below of triangle ABC, CDA, CEB, DE || AB, DE = 4,
AB = 10, CD = x, and DA = x + 3.
What is the value of x?
(4) 6. Set-up the proportion CD/DE = CA/AB
x / 4 = (2x + 3) / 10. (Don't forget to add x and x + 3.)
10x = 8x +12
2x = 12
x = 6.
27. Given: AE bisects BD at C
AB and DE are drawn
<ABC = <EDC
Which statement is needed to prove ABC = EDC using ASA?
(3) <BCA = <DCE. You are given a pair of angles. The bisecting gives the included side. The two vertical angles are the other pair of angles.
28. In the construction shown below, CD is drawn.
In triangle ABC, CD is the
(2) median to side AB. From the marks, a perpendicular bisector of AB was constructed. Point D is therefore the midpoint of AB, making CD the median.
End of Part I.
Wednesday, February 17, 2016
Qo'nos
Does the food make you go, "Gagh!"?
I've actually never been to a Quiznos, nor know if they have drive-thrus.
But I'd like to see a Klingon alternative called Qo'nos.
Come back often for more funny math and geeky comics.
Monday, February 15, 2016
Valentine Reflections
It was already broken. He just didn't make it whole.
Yeah, this should've gone up a few days ago. Still works though.
And Happy Presidents Day.
Come back often for more funny math and geeky comics.
Thursday, February 11, 2016
(x, why?) Mini: Flowers
Thinking of Spring and flowers . . .
And, oddly, I thought I could reuse old artwork for a quick comic. And I hated it, so I replaced the old artwork with new artwork. These
"minis" are sometimes as time-consuming as the regular ones.
Come back often for more funny math and geeky comics.
Wednesday, February 10, 2016
Music Venn Diagram
The views expressed in the diagram reflect the opinions of the comic makers in so far as there are four possibilities expressed in the comic.
The fourth possibility is left as an exercise for the reader (but should be really, really obvious).
Come back often for more funny math and geeky comics.
Tuesday, February 09, 2016
January 2016 New York Geometry (Common Core) Parts 3 and 4
Below are the questions with answers and explanations for Parts 3 and 4 of the Geometry (Common Core) Regents exam for January 2016. Part I questions appeared in a here. Part II questions appeared in a Here.
Part III
Question 32 was answered in the post for Part II. It is reprinted here because it was actually a Part III question.
32. The aspect ratio (the ratio of screen width to height) of a rectangular flat-screen television I s16:9. The length of the diagonal of the screen is the television’s screen size. Determine and state, to the nearest inch, the screen size (diagonal) of this flat-screen television with a screen height of 20.6 inches.
This can be solved using ratios and Pythagorean Theorem, or by using Trigonometric Ratios.
First, set up a proportion 16/9 = x/20.6 and cross-multiply.
9x = 329.6, x = 36.6
20.62 + 36.62 = c2
424.36 + 1339.56 = c2
1763.02 = c2
C = 41.999 = 42 inches
Second, the ratio 16:9 represents the opposite over the adjacent, which is the tangent of the top angle of the set. So tan(y) = 16/9 and y = tan-1(16/9) = 60.64 degrees.
Using the adjacent and the hypotenuse and cosine, we get the following:
cos(60.64) = 20.6/x, so x = 9/cos(60.64) = 42.0155… = 42 inches.
33. Given the theorem, "The sum of the the measures of the interior angles of a triangle is 180o," complete the proof for this theorem.
Fill in the missing reasons below.
This problem caused students a bit of trouble. First, many students had no idea what to write as a reason for Statement (2). What they wrote might have been a correct statement, but not a correct reason for the statement that was made. There is a difference between the two.
Another problem is that many students gave the reason that "The sum of the angles of a triangle is 180 degrees." While this is a true statement, it cannot be used as a Reason when that is exactly what you are trying to prove!
Most of the papers I graded score only 2 of the 4 points. (One point for each correct reason. "Given" was preprinted.)
(1) Triangle ABC. Given
(2) Through point C, draw DCE parallel to AB. Through any line and a point not on the line, there is exactly one line passing through that point parallel to the line.
(3)m<l = m<ACD, m<3 = m<BCE When two parallel lines are cut by a transversal, alternate interior angles are congruent.
(4) m<ACD + m<2 + m<BCE = 180° The sum of angles creating a straight line is 180 degrees.
(5) mLl + mL2 + mL3 = 180° Substitution Property
I saw many students who didn't label angles as "alternate interior", leaving out one word or the other. And a number of them mentioned supplementary angles in statement (4), but "supplementary" applies to two angles, not three.
34. Triangle XYZ is shown below. Using a compass and straightedge, on the line below, construct and label triangle ABC, such that triangle ABC = triangle XYZ. [Leave all construction marks.]
Based on your construction, state the theorem that justifies why triangle ABC is congruent to triangle XYZ.
Sorry, but I can't illustrate constructions very well. I promise to get back to it.
Simple steps: From point X, measure the distance to Y. On the line, make point A and mark the distance to with an arc, and label where the arc intersects the line as B. Go back to X and measure the distance to Z. Go to X and make another arc. Go back to Y and measure the length to Z. Put the compass on B and make an arc. Where the two arcs intercept, label that point C. Using the straightedge, make lines AC and BC. The theorem used was SSS.
Note: It is possible that you could have used SAS to create the triangles. Whichever theorem you stated, the construction marks had to match it to get full credit.
You also could have gotten 1 point for saying SSS, SAS, or ASA without any construction at all.
Part IV
35. Given: Parallelogram ANDR with AW and DE bisecting NWD and REA at points W and E, respectively
Prove that triangle ANW = triangle DRE.
Prove that quadrilateral AWDE is a parallelogram.
There are many variations of this proof which will be acceptable. When using SAS to prove two triangles congruent, be sure that you have included statements regarding the two pairs of sides and the included pairs of angles.
(1) Parallelogram ANDR with AW and DE bisecting NWD and REA. Given
(2) AE = RE and DW = NW Definition of segment bisector.
(3) RA = DN and RD = NA Opposite sides of a parallelogram are congruent.
(4) RE = NW Halves of congruent segments are congruent.
(5) Angle R = Angle N Opposite angles of a parallelogram are congruent.
(6) Triangle DRE = Triangle ANW SAS
(7)ED = WA CPCTC
(8)AE = DW Halves of congruent segments are congruent.
(9) AWDE is a parallelogram If both pairs of opposite sides of a quadrilateral are congruent, then the quadrilateral is a parallelogram
Parallelograms have many properties that apply only to them. Proving any of those would be sufficient proof that AWDE was a parallelogram.
36. Cathy wants to determine the height of the flagpole shown in the diagram below. She uses a survey instrument to measure the angle of elevation to the top of the flagpole, and determines it to be 34.9°. She walks 8 meters closer and determines the new measure of the angle of elevation to be 52.8°. At each measurement, the survey instrument is 1.7 meters above the ground.
Determine and state, to the nearest tenth of a meter, the height of the flagpole.
Personally, I hate problems that force you to add 1.7 meters at the end for no good reason. It's just an added step for people to forget about and lose a point.
One also wonder why Cathy didn't walk to the pole and measure that distance rather than walking an extra 8 meters away from it. But this is the problem we are given.
We are looking for the height of the pole. That is the opposite side to both angles. We have some information about the distance along the ground. That is the adjacent side to the angles. We have no information about the hypotenuse, nor are we looking for it.
Opposite and adjacent means that we are using tangent.
Let h be the height and x be the distance along the ground to the first measurement.
tan 52.8 = h / x
so h = x (tan 52.8)
And tan 34.9 = h / (x + 8)
so h = (x + 8)(tan 34.9)
This means that x (tan 52.8) = (x + 8)(tan 34.9). We need to isolate x.
Distribute: x (tan 52.8) = x (tan 34.9) + 8(tan 34.9)
Subtract: x (tan 52.8) - x (tan 34.9) = 8(tan 34.9)
Factor: x (tan 52.8 - tan 34.9) = 8(tan 34.9)
Divide: x = 8(tan 34.9) / (tan 52.8 - tan 34.9)
Calculate: x = 9.00371 = 9 meters
Use x to get h:
h = 9.00371(tan 52.8) = 11.8619
And the height of the survey instrument: 11.86 + 1.7 = 13.56 = 13.6 meters.
An amazing amount of work, but it was worth 6 points.
You lost credit if you forgot the 1.7 meters, used the wrong functions, or rounded in the middle of the problem so that your answer didn't round to 13.6
Oddly, if you multiplied 1.7 * 8 you get EXACTLY 13.6. If you wrote 13.6 with NO WORK WHATSOEVER, you got one point. If you wrote 1.7 * 8 = 13.6, you got ZERO POINTS for a totally incorrect response or a correct response found through a totally incorrect method. Those are the breaks.
END OF PART IV.
How did you do?
Monday, February 08, 2016
January 2016 New York Geometry (Common Core) Part 1
Below are the questions with answers and explanations for Part 1 the Geometry (Common Core) Regents exam for January 2016. Part II questions appeared in a another post.
Part I
1. William is drawing pictures of cross sections of the right circular cone below. (image omitted)
Which drawing can not be a cross section of a cone?
(1) the square. You can make a slice through that cone and get an oval (or circle), a semicircle with a diameter on the bottom or even triangle if you split it vertically. You can't get a square.
2. An equation of a line perpendicular to the line represented by the equation y = -(1/2)x - 5 and passing through (6, -4) is
(4) y = 2x - 16. A line perpendicular to a line with a slope of -1/2 would have a slope of 2, so (1) and (2) are out. If you plug in 6 for x, -4 = 2(6) + b, b = -16.
3. In parallelogram QRST shown below, diagonal TR is drawn, U and V are points on TS and QR, respectively, and UV intersects TR at W.
If m<S = 60°, m<SRT = 83°, and m<TWU = 35°, what is m< WVQ?
(3) 72°. Look at quadrilateral QTWV, which has 360°. Angle Q = S = 60. Angle QTV = SRT = 83. Angle TWV = 180 - TWU = 180 - 35 = 145. 60 + 83 + 145 = 288. 360 = 288 = 72°.
4. A fish tank in the shape of a rectangular prism has dimensions of 14 inches, 16 inches, and 10 inches. The tank contains 1680 cubic inches of water. What percent of the fish tank is empty?
(2) 25. The volume of the tank is 14 * 16 * 10 = 2240. 2240 - 1680 = 560 gallons empty. 560 / 2240 = .25 = 25%
5. Which transformation would result in the perimeter of a triangle being different from the perimeter of its image?
(3) (x,y)--> (4x,4y). A dilation would change the distance between the vertices, and therefore the perimeter. Reflections and translations do not affect the size, so the image would have the same perimeter.
6. In the diagram below, FE bisects AC at B, and GE bisects BD at C.
Which statement is always true?
(1) AB = DC. Because of bisecting AB = BC and BC = CD. Therefore, AB = CD. We have no information about where points F or G are, so you cannot make any assumptions about those lines being bisected or the segments being equal.
7. As shown in the diagram below, a regular pyramid has a square base
whose side measures 6 inches. (image omitted)
If the altitude of the pyramid measures 12 inches, its volume, in cubic inches, is
(2) 144. The Volume is (1/3)(Area of the Base)(height) = (1/3)(6 * 6)(12) = (12)(12) = 144.
8. Triangle ABC and triangle DEF are graphed on the set of axes below.
Which sequence of transformations maps triangle ABC onto
triangle DEF?
(1) a reflection over the x-axis followed by a reflection over the y-axis. It is also a 180 degree rotation about the origin, but it would NOT be followed by a reflection in y = x.
9. In triangle ABC, the complement of <B is <A. Which statement is always true?
(4) sin <A =cos <B. The sine of one complementary angle is the cosine of the other in a right triangle. The side opposite angle A will be adjacent to angle B.
10. A line that passes through the points whose coordinates are (1,1) and (5,7) is dilated by a scale factor of 3 and centered at the origin. The image of the line
(2) is parallel to the original line. As long as the line does not go through the origin, its dilation will be a parallel line (having the same slope). If the line went through the origin, it would be the same line. The slope of the line is 6/4 = 3/2. The line y = 3/2x does not go through (1, 1), so the line being dilated does not go through the origin.
11. Quadrilateral ABCD is graphed on the set of axes below.
When ABCD is rotated 90° in a counterclockwise direction about
the origin, its image is quadrilateral A' B 'C 'D'. Is distance preserved
under this rotation, and which coordinates are correct for the given
vertex?
(4) yes and B'(-3,4) . Yes, distance is preserved, (1) and (2) are eliminated. A(-2, 6) will move to A'(-6, -2). Choice (3) would have been correct for a clockwise rotation.
12. In the diagram below of circle 0, the area of the shaded sector LOM
is 2(pi) cm2.
If the length of NL is 6 cm, what is m<N?
(3) 40°. The diameter is 6 cm, so the radius is 3 cm. That makes the Area of the entire circle = (pi)(3)2 = 9pi.
if the shaded sector is 2pi, then that sector and that arc is 2/9 of the circle, which is 2/9(360) = 80 degrees. Angle N is an inscribed angle that intercepts arc LM, so it is half of 80 degrees, or 40 degrees.
13. In the diagram below, triangle ABC ~ triangle DEF.
If AB = 6 and AC = 8, which statement will justify similarity by SAS?
(1) DE = 9, DF = 12, and <A = <D. Angles A and D are the included angles, so (3) and (4) are eliminated. 6/8 = .75 and 9/12 = .75, so they are proportional.
14. The diameter of a basketball is approximately 9.5 inches and the diameter of a tennis ball is approximately 2.5 inches. The volume of the basketball is about how many times greater than the volume of the tennis ball?
(3) 55. The radius of the basketball is 4.75. The radius of the tennis ball is 1.25. Volume requires cubing the radii. Divide (4.753 / 1.253) = 54.872, which is approximately 55.
15. The endpoints of one side of a regular pentagon are (-1,4) and (2,3). What is the perimeter of the pentagon?
(2) 5*SQRT(10). Using the Distance formula (or the Pythagorean Theorem), we can find the length of the segment joining those two endpoints to be SQRT(32 + 12), which is SQRT(10). Since there are five sides to a pentagon, the perimeter is 5*Sqrt(10). [5 radical 10]
16. In the diagram of right triangle ABC shown below, AB = 14 and AC= 9. (image omitted)
What is the measure of <A, to the nearest degree?
(3) 50. AC is the adjacent side and AB is the hypotenuse, so cos A = 9/14. That means <A = cos-1(9/14) = 49.99... degrees.
17. What are the coordinates of the center and length of the radius of the circle whose equation is x2 + 6x + y2 - 4y = 23?
(4) (-3,2) and 6 You need to complete the squares to find the equation for the circle. (I could make a comic out of that sentence.)
Half of +6 is +3, and half of -4 is -2, but you have to flip the signs to find (h, k). Remember: (x - h)2 + (y - k)2.
So the center is at (-3, 2) and you eliminate (1) and (2).
To complete the square you need to add (3)2 add (-2)2 to both sides of the equations. That adds 9 + 4 to 23, giving 36, which is r2. So the radius is 6 (not 36).
18. The coordinates of the vertices of triangle RST are R(-2, -3), S(8,2), and T(4,5). Which type of triangle is triangle RST?
(1) right. Eliminate (4) equiangular, because equiangular/equilateral triangles are always acute, and you can't have two correct answers.
If the triangle is right, then two of the sides will have perpendicular slopes -- that is, they will be negative reciprocals. If that is not true, then you have to find the lengths of the three sides to determine if the triangle is acute or obtuse.
Slope of RS = (2 - -3)/(8 - -2) = 5/10 = 1/2. Slope of ST = (5 - 2)/(4 - 8) = 3/(-4) = -(3/4). Slope of TR = (-3 - 5)/(-2 - 4) = -8/-6 = 4/3. ST is perpendicular to TR because (-3/4)(4/3) = -1. It is a right triangle.
19. Molly wishes to make a lawn ornament in the form of a solid sphere. The clay being used to make the sphere weighs .075 pound per cubic inch. If the sphere's radius is 4 inches, what is the weight of the sphere, to the nearest pound?
(2) 20. Multiply the Volume of the sphere by .075, so .075(4/3)(pi)(4)3 = 20.1..., which is about 20.
20. The ratio of similarity of triangle BOY to triangle GRL is 1:2. If BO = x + 3 and GR = 3x - 1, then the length of GR is
(4) 20. Because GR is twice as big as BO, start with 2(x + 3) = 3x - 1,
So 2x + 6 = 3x - 1
and 7 = x. (note that this is choice (2).)
The length of GR is 3(7) - 1 = 20.
21. In the diagram below, DC, AC, DOB, CB, and AB are chords of circle O, FDE is tangent at point D, and radius AO is drawn. Sam decides to apply this theorem to the diagram: "An angle inscribed in a semi-circle is a right angle."
Which angle is Sam referring to?
(3) <DCB. DOB is a diameter of the triangle and arc DAB is a semi-circle. Angle DCB is an inscribed angle that intercepts the semi-circle. Since it is half the measure of the 180 degrees, it must be 90 degrees, making it a right angle.
22. In the diagram below, CD is the altitude drawn to the hypotenuse AB
of right triangle ABC. (image omitted)
Which lengths would not produce an altitude that measures 6*SQRT(2)?
(2) AD = 3 and AB = 24 Square (6*SQRT(2)) and you get 36 * 2 = 72 as the altitude. The product of AD and DB must be 72 for the altitude to be 6*SQRT(2). Read the choices carefully. Two of the choices give you AB, not DB. You need to subtract AD from AB to get DB. While 3 * 24 equals 72, you are supposed to be multiplying 3 * 21, which is only 63.
23. A designer needs to create perfectly circular necklaces. The necklaces each need to have a radius of 10 cm. What is the largest number of necklaces that can be made from 1000 cm of wire?
(1) 15. If the radius is 10 cm, then the length of the wire to produce one necklace, (2)(10)(pi), is approximately 62.83 cm. Divide 1000/62.83 and you get 15.9. However, you cannot round up because you don't have enough wire to finish the 16th necklace.
24. In triangle SCU shown below, points T and O are on SU and CU, respectively. Segment OT is drawn so that <C = <OTU.
If TU = 4, OU = 5, and OC = 7, what is the length of ST?
(3) 11. Triangles OUT and CUS are similar, and the sides are proportional, but make sure you set up the proportion correctly. OT is NOT parallel to CS. The correct proportion is 4/(7 + 5) = 5/(4 + x), so 16 + 4x = 60.
4x = 44, x = 11.
END OF PART 1.
I also write Fiction!Check out In A Flash 2020, by Christopher J. Burke for 20 great flash fiction stories, perfectly sized for your train rides. Available in softcover or ebook at Amazon. If you enjoy it, please consider leaving a rating or review on Amazon or on Good Reads. Thank you. |
 |
Year of the Monkey
For the record, Xiu is *not* an immortal. That I know of.
He still gets around very well, and he might outlast me. And ... hmmmm....
Happy New Year 4713!
Come back often for more funny math and geeky comics.
Sunday, February 07, 2016
Super Bowl 50
Let the discussion of Ordinal v. Cardinal begin now.
Seriously, I get comments from people who get it backward and/or think I got it backward. As for our buddy, L in the comic, he is refering to last year's comic.
Come back often for more funny math and geeky comics.