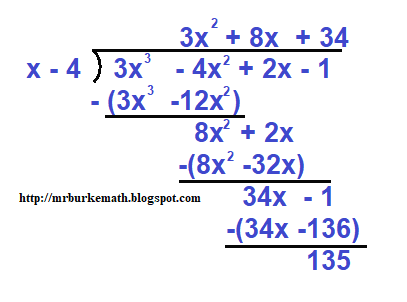This exam was adminstered in August 2022. These answers were not posted until they were unlocked on the NY Regents website or were posted elsewhere on the web.
More Regents problems.
Algebra 2 August 2022
Part III: Each correct answer will receive 4 credits. Partial credit can be earned. One computational mistake will lose 1 point. A conceptual error will generally lose 2 points (unless the rubric states otherwise). It is sometimes possible to get 1 point for a correct answer with no correct work shown.
33. When observed by researchers under a microscope, a smartphone screen contained approximately
11,000 bacteria per square inch. Bacteria, under normal conditions, double in population every 20
minutes.
a) Assuming an initial value of 11,000 bacteria, write a function, p(t), that can be used to model the
population of bacteria, p, on a smartphone screen, where t represents the time in minutes after it
is first observed under a microscope.
b) Using p(t) from part a, determine algebraically, to the nearest hundredth of a minute, the arr;iount
of time it would take for a smartphone screen that was not touched or cleaned to have a population
of 1,000,000 bacteria per square inch.
Answer:
The starting values is 11,000. The base is 2 because it's doubling. The exponent is t/20 because t is measured in minutes but it's doubling every 20 minutes.
So the function would be:
p(t) = 11,000(2)(t/20)
The "p(t) = " is mandatory. If you only write the expression, you will not receive credit.
In the part b, replace p(t) with 1,000,000 and solve for t using logs.
p(t) = 11,000(2)(t/20)
1,000,000 = 11,000(2)(t/20)
1,000,000/11,000 = (2)(t/20)
log 90.90909 = log (2)(t/20)
log 90.90909 = t/20 log 2
t = 20 log 90.90909 / log 2 = 130.1275...
t = 130.13 minutes
34. The function v(x) = x(3 - x)(x + 4) models the volume, in cubic inches, of a rectangular solid for
0 ≤ x ≤ 3.
Graph y = v(x) over the domain 0 ≤ x ≤ 3.
To the nearest tenth of a cubic inch, what is the maximum volume of the rectangular solid?
Answer:
Use your calculator, but plot every 0.2. If you only plot (0,0), (1,10), (2,12) and (3,0), you won't have the actual maximum. Also, this is part of a cubic function. It will not be a parabola even though you might think from the interval selected that it should look like one.
When you have plotted the points, you'll get a graph that looks something like:
To the nearest tenth, the maximum is about 12.6.
35. Given f(x) = 3x3 - 4x2 + 2x - 1 and g(x) = x - 4, state the quotient and remainder of f(x)/g(x) in the form q(x) + r(x)/g(x).
Is x = 4 a root of f(x)? Explain your answer.
Answer:
The form means that they want it as a polynomial plus a remainder divided by (x - 4). For the second part, x = 4 won't be a root of f(x) unless there is no remainder when dividing by (x - 4). From the wording of the question, it's fairly certain that there will be a remainder and that x = 4 is not a root.
Look at the image below that shows polynomial long division:
The quotient is 3x2 + 8x + 34 + 135 / (x - 4).
Since (x - 4) is not a factor of the f(x) -- there is a remainder -- then x = 4 cannot be a root to f(x).
You can also calculate f(4). It doesn't equal 0, so it isn't a root.
Alternatively, you could have shown the division as follows:
Just remember to use 4 and not -4, and write the resulting polynomial.
36. State officials claim 82% of a community want to repeal the 30 mph speed limit on an expressway.
A community organization devises a simulation based on the claim that 82% of the community
supports the repeal. Each dot on the graph below represents the proportion of community
members who support the repeal. The graph shows 200 simulated surveys, each of sample size 60.
Based on the simulation, determine an interval containing the middle 95% of plausible proportions.
Round your answer to the nearest thousandth.
The community organization conducted its own sample survey of 60 people and found 70%
supported the repeal. Based on the results of the simulation, explain why the organization should
question the State officials’ claim.
Answer:
The interval containing the middle 95% of the data would be within 2 standard deviations above and below the mean.
0.819 - 2(.053) = 0.713 and 0.819 + 2(.053) = 0.925, so the interval is 0.713 - 0.925.
They should question the claim because 70% is outside the 71.3% - 92.5% range, which is the 95% interval.
End of Part III
How did you do?
More to come. Comments and questions welcome.
More Regents problems.
I also write Fiction!
You can now preorder Devilish And Divine, edited by John L. French and Danielle Ackley-McPhail, which contains (among many, many others) three stories by me, Christopher J. Burke about those above us and from down below.
Preorder the softcover or ebook at Amazon.
Also, check out In A Flash 2020, by Christopher J. Burke for 20 great flash fiction stories, perfectly sized for your train rides.
Available in softcover or ebook at Amazon.
If you enjoy it, please consider leaving a rating or review on Amazon or on Good Reads.
|
 |
 |