This exam was adminstered in August 2022. These answers were not posted until they were unlocked on the NY Regents website or were posted elsewhere on the web.
August 2022 Geometry, Part II
Each correct answer is worth up to 2 credits. Partial credit can be given. Work must be shown or explained.
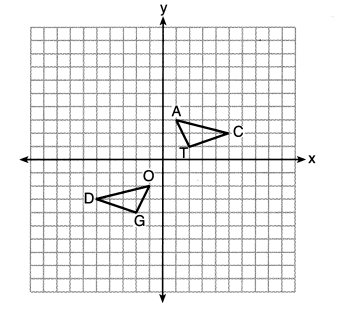
25.
On the set of axes below, △DOG ≅ △CAT
Describe a sequence of transformations that maps △DOG onto △CAT.
Answer:
There are a few possible answers.
First, a reflection over the y-axis follow by translation 5 units up. Second, you could do that in the opposite order.
It is possible to reflect over different vertical or horizontal lines and then translate the image until it maps onto CAT.
A rotation would not work. The image would not be oriented correctly.
26. In right triangle MTH shown below, m∠H = 90°, HT = 8, and HM = 5.
Determine and state, to the nearest tenth, the volume of the three-dimensional solid formed by
rotating △MTH continuously around MH.
Answer:
The three-dimensional solid will be a cone. The volume of a cone is given by the formula V = 1/3 πr2h.
V = 1/3 πr2h = 1/3 π (8)2 (5) = 335.10...
V = 335.1
27. Using a compass and straightedge, dilate triangle ABC by a scale factor of 2 centered at C.
[Leave all construction marks.]
Answer:
This has to be one of the simplest construction problems that I have ever seen used.
Using the straightedge, extend line CA past A and extend line CB past B.
Use the compass and measure CA. Move to point A and make a mark on the extended line that is the same length.
Repeat this for CB.
Use the straightedge to draw the third side of the triangle.
You could also draw a circle around A with radius AC and a circle around B with radius BC.
28. A rock-climbing wall at a local park has a right triangular section that slants toward the climber,
as shown in the picture below. The height of the wall is 5 meters and the slanted section begins
1.2 meters up the wall at an angle of 14 degrees.
Determine and state, to the nearest hundredth, the number of meters in the length of the
section of the wall that is slanted (hypotenuse).
Answer:
This questions seems more complicated that it actually is. Label the photo and you will see that the leg of the triangle is 3.8, because it is 5 - 1.2. They want the hypotenuse and they have given you the side adjacent to the angle. That means you need to use Cosine.
Cos 14 = 3.8 / x
x = 3.8 / Cos 14 = 3.916... = 3.92.
29. In the diagram below of right triangle BAL, altitude
AD is drawn to hypotenuse.
The length of AD is 6.
If the length of DL is four times the length of BD, determine and state the length of BD.
Answer:
The Right Triangle Altitude Theorem says that (AD)2 = (BD)(DL), and we know that DL = 4(BD).
62 = x(4x)
4x2 = 36
x2 = 9
x = 3
BD = 3.
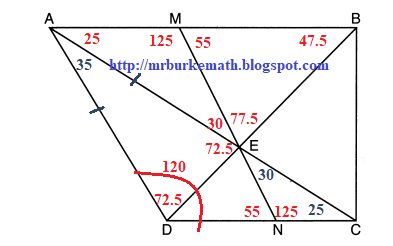
30.
Trapezoid ABCD, where AB || CD, is shown below. Diagonals AC and DB intersect MN at E, and AD ≅ AE.
If m∠DAE = 35°, m∠DCE = 25°, and m∠NEC = 30°, determine and state m∠ABD.
Answer:
Label what you know and calculate angles until you get to ABD. Since AD ≅ AE, then m∠ADE = m∠AED = 72.5. Vertical angles are congruent. Alternate interior angles are congruent. The sum of the angles of a triangle is 180.
Look at the image below:
m∠ABD = 47.5
31.
In the diagram below of circle 0, the measure of inscribed angle ABC is 36° and the length of
OA is 4 inches.
Determine and state, to the nearest tenth of a square inch, the area of the shaded sector.
Answer:
The inscribed angle is 36 degrees, so the central angle is twice as big, or 72 degrees.
The area of the sector of the circle is A = (72/360) πr2.
A = (72/360) (3.141592) (4)2 = 10.053... = 10.1
End of Part II
How did you do?
Questions, comments and corrections welcome.
I also write Fiction!You can now order Devilish And Divine, edited by John L. French and Danielle Ackley-McPhail, which contains (among many, many others) three stories by me, Christopher J. Burke about those above us and from down below. Preorder the softcover or ebook at Amazon. Also, check out In A Flash 2020, by Christopher J. Burke for 20 great flash fiction stories, perfectly sized for your train rides. Available in softcover or ebook at Amazon. If you enjoy it, please consider leaving a rating or review on Amazon or on Good Reads. |
 |
 |