Now that I'm caught up with the current New York State Regents exams, I'm revisiting some older ones.
More Regents problems.
Algebra 2/Trigonometry Regents, June 2011
Part I: Each correct answer will receive 2 credits.
6. What is the value of x in the equation log5 x = 4?
1) 1.16
2) 20
3) 625
4) 1,024
Answer: 3) 625
If log base 5 of x is 4 then 5 to the power of 4 is x.
54 = 625, which is choice (3).
Choice (1) is the approximate answer to 4x = 5.
Choice (2) is just 4 times 5.
Choice (4) is 45, if you reversed the expression that you wanted.
7. The expression 4√(16x2y7 is equivalent to
1) 2x1/2y7/4
2) 2x8y28
3) 4x1/2y7/4
4) 4x8y28
Answer: 1) 2x1/2y7/4
The fourth root of 16 is 2 because 24 = 16. Eliminate Choices (3) and (4).
The 4th root is the same as taking the 1/4 power, so divide the exponents under the radical by 4, and you get 1/2 and 7/4. This is Choice (1).
DON'T multiply them.
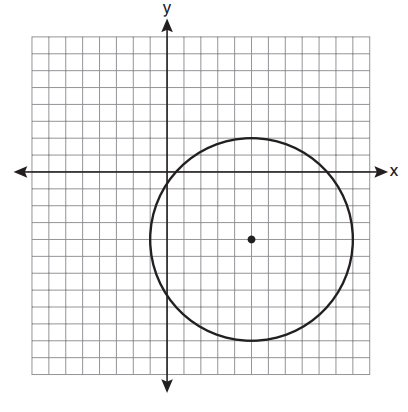
8. Which equation is represented by the graph below?
1) y = 5x
2) y = 0.5x
3) y = 5-x
4) y = 0.5-x
Answer: 2) y = 0.5x
Choices (1) and (4) would both be increasing functions, not decreasing, so eliminate them.
(0.5)x = (1/2)x and (5)-x = (1/5)x
If you look at x = -1, y = 2, and (1/2)(-1) = 2. The answer is Choice (1).
9. What is the fifteenth term of the geometric sequence −√(5), √(10), −2√(5), . . . ?
1) −128√(5)
2) 128√(10)
3) −16384√(5)
4) 16384√(10)
Answer: 1) −128√(5)
The common ratio in the sequence is √(10)/-√(5) = -√(2). First, you can see that the 15th term will be negative, so eliminate Choices (2) and (4).
The 50th term would be -√(5)*(-√(2))14, which is -√(5)*(2)7, which is -128√(5).
10. In △ABC, a = 15, b = 14, and c = 13, as shown in the diagram below.
What is the m∠C, to the nearest degree?
1) 53
2) 59
3) 67
4) 127
Answer: 1) 53
The angle across from the smallest side is the smallest angle. The triangle is 13-14-15, which is almost equilateral, so the angles are close to 60, but angle C must be smaller than 60. Eliminate Choices (3) and (4).
The question is does the difference in sides reduce the angle all the way down to 53 degrees? My hunch before working out this problem is that 53 is way more likely than 59.
Since we don't know any of the angles, we aren't going to use the Law of Sines. Instead, we'll use the Law of Cosines
cos(C) = (a2 + b2 − c2) / (2ab)
cos(C) = (152 + 142 − 132) / (2(14)(15))
cos(C) = 3/5
C = cos-1 3/5 = 53.1 degrees
Looks like my hunch was good, but I'm glad I worked it out anyway.
More to come. Comments and questions welcome.
More Regents problems.
I also write Fiction!You can now preorder Devilish And Divine, edited by John L. French and Danielle Ackley-McPhail, which contains (among many, many others) three stories by me, Christopher J. Burke about those above us and from down below. Preorder the softcover or ebook at Amazon. Also, check out In A Flash 2020, by Christopher J. Burke for 20 great flash fiction stories, perfectly sized for your train rides. Available in softcover or ebook at Amazon. If you enjoy it, please consider leaving a rating or review on Amazon or on Good Reads. |
 |
 |