The following are some of the multiple questions from the recent June 2018 New York State Common Core Geometry Regents exam.
Each correct answer is worth up to 2 credits. No partial credit. Work need not be shown.
1. After a counterclockwise rotation about point X, scalene
triangle ABC maps onto triangle RST, as shown in the diagram below.
Answer: (1) ∠A = ∠R
2. In the diagram below, AB || DEF, AE and BD intersect at C,
m∠B = 43°, and m∠CEF = 152°.
Answer: (3) m∠ACD = 71°
3. In the diagram below, line m is parallel to line n. Figure 2 is the image
of Figure 1 after a reflection over line m. Figure 3 is the image of
Figure 2 after a reflection over line n.
Answer: (4) a translation
4. In the diagram below, AF and DB intersect at C, and AD and FBE
are drawn such that m∠D = 65°, m∠CBE = 115°, DC = 7.2, AC = 9.6, and FC = 21.6.
Answer: (3) 16.2
5. Given square RSTV, where RS = 9 cm. If square RSTV is dilated by
a scale factor of 3 about a given center, what is the perimeter, in centimeters, of the image of RSTV after the dilation?
Answer: (4) 108
6. In right triangle ABC, hypotenuse AB has a length of 26 cm, and
side BC has a length of 17.6 cm. What is the measure of angle B, to the nearest degree?
Answer: (2) 47°
7. The greenhouse pictured below can be modeled as a rectangular
prism with a half-cylinder on top. The rectangular prism is 20 feet wide, 12 feet high, and 45 feet long. The half-cylinder has a diameter
of 20 feet.
Answer: (1) 17,869
8. In a right triangle, the acute angles have the relationship
sin (2x + 4) = cos (46).
What is the value of x?
Answer: (1) 20
June 2018 Geometry, Part I
Which statement must be true?
A rigid motion, such as a rotation, does not change size, so the corresponding angles and sides remain the same.
Angle A corresponds to Angle R. Angle B corresponds to Angle S. Angle C corresponds to Angle T.
Choice 2 does not have corresponding angles. Choices 3 and 4 do not have corresponding sides.ity symbol.
Which statement is true?
Because of alternate interior angles, angle D = 43 degrees. Angle CED is supplementary to 152 degrees, so it must be 180 - 152 = 28 degrees.
By the Exterior Angle Theorem, Angle ACD must be the sum of the two remote angles, D and CED. So 43 + 28 = 71 degrees.
Which single transformation would carry Figure 1 onto Figure 3?
A translation will move Figure 1 directly to Figure 3. Reflecting the figure switched the orientation, but reflecting it a second time switched it back to its original orientation.
A dilation would have increased its size. A rotation would have changed its orientation, as would a single reflection.
What is the length of CB?
If angle DBE = 115 degrees, then angle DBF = 65 degrees. This makes angles DBF and D congruent. Angles ACD and BCF are congruent because they are vertical angles. Therefore, the two triangles are similar. (Of course, if these triangles weren't similar to begin with, this would've been a much harder problem to deal with!)
That means that the corresponding sides are proportional.
7.2 / 9.6 = x / 21.6
9.6x = (7.2)(21.6)
x = (7.2)(21.6)/9.6 = 16.2
If RS = 9, then the perimeter is 9 * 4 = 36. If the square is dilated by a factor of 3, then the perimeter will be 3 times as much. So 36 * 3 = 108.
Alternatively, 9 * 3 = 27 cm as the length of the side of the image, and 27 * 4 = 108.
cos B = 17.6 / 26
B = cos-1 (17.6/26) = 47.396... or 47 degrees.
To the nearest cubic foot, what is the volume of the greenhouse?
The Volume of the rectangular prism is Length x Width x Height. The volume of the half-cylinder is 1/2 pi x radius2 x height. Don't confuse to two things that are labeled "height".
Vp = (12)(20)(45) = 10800
Vc = (1/2)(10)2(pi)(45) = 7068.583...
For a total of approximately 17,869
In a right triangle, the relationship between sin and cos of the acute angles is as follows:
2x + 4 = 44
2x = 40
x = 20
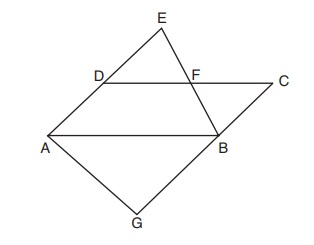
9. In the diagram below, AB||DFC, EDA||CBG, and EFB and AG are drawn.
Which statement is always true?
Answer: (4) Triangle DEF ~ Triangle AEB
Because AB || EDF then Angle A = Angle EDF, and angle E is congruent to itself by the Reflexive Property. By AA, triangles DEF and AEB are similar.
Of the incorrect answers, choice (1) would have been correct had it said "similar to" and not "congruent to", because of alternate interior angles and vertical angles. However, there is no indication that F is the midpoint of EB or CD, or that BC is congruent to DE.
10. The base of a pyramid is a rectangle with a width of 4.6 cm and a length of 9 cm. What is the height, in centimeters, of the pyramid if its volume is 82.8 cm3?
Answer: (1) 6
The formula for the Volume of a rectangular-based pyramid is V = 1/3 L * W * H.
So 82.8 = (1/3) * (4.6) * (9) * H.
And H = 82.8 / ((1/3) * (4.6) * (9))
H = 6 cm.
11. In the diagram below of right triangle AED, BC || DE.
Which statement is always true?
Answer: (2) AB/AD = BC/DE
Short hypotenuse / Long hoptenuse = Short altitude / Long altitude
The incorrect choices:
(1) Short base / Long base =/= Long altitude / Short altitude -- incorrect order
(3) Short base / *segment* of long base =/= Short altitude / Long altitude -- not corresponding parts
(4) Long altitude / Short altitude =/= *segment* of long hypotenuse / Short hypotenuse -- not corresponding parts
12. What is an equation of the line that passes through the point (6,8) and is perpendicular to a line with equation y = 3/2 x + 5?
Answer: (2) y - 8 = - 2/3 (x - 6)
Perpendicular means that the slope of the new line is -2/3, so eliminate choices (1) and (3), which are parallel.
Point-slope form is y - y0 = m(x - x0). Note the signs.
Plug in 6 for x0 and 8 for y0
13. The diagram below shows parallelogram ABCD with diagonals and intersecting at E.
What additional information is sufficient to prove that parallelogram
ABCD is also a rhombus?
Answer: (4) AC is perpendicular to BD
The diagonals of a rhombus are perpendicular to each other.
Choices (1), (2), and (3) are true for all parallelograms, not just rhombuses.
14. Directed line segment DE has endpoints D(-4,-2) and E(1,8). Point F divides such that DF:FE is 2:3. What are the coordinates of F?
Answer: (1) (-2,2)
2 + 3 = 5, so point F is 2/5 of the way from D to E.
1 - (-4) = 5, and (2/5)(5) = 2. Add 2 to -4 and you get -2, which must be the x-coordinate for F. So Choice (2).
8 - (-2) = 10, and (2/5)(10) = 4. Add 4 to -2 and you get 2, which must be the y-coordinate for F. Still Choice (2).
Notice that point F must be on the line BETWEEN D and E, so Choice (4) makes no sense at all.
15. Triangle DAN is graphed on the set of axes below. The vertices of
DAN have coordinates D(-6,-1), A(6,3), and N(-3,10).
What is the area of triangle DAN?
Answer: (1) 60
Reason this one out. It's a multiple-choice question, so you don't have to go the long way.
You might notice that the slope of DA is 1/3. That means that the altitude of the triangle can be found by starting at N(-3, 10) and finding points that are 3 down and 1 to the right, because the perpendicular slope is -3. This gives you the point (0, 1). Call it P.
You could then find the length of AD and NP, and then use those vales as base and height in the formula (1/2) b h.
HOWEVER, there is another way. Make a big rectangle around the triangle, so that D, A, and N are each touching a side of the rectangle.
This rectangle with have dimensions 11 X 12, or 132 square units.
Now remove the "negative" space -- that is, the three triangles outside of DAN.
First thing you will realize is that all the bases and heights are whole numbers, so their areas are rational. That means that choices (3) and (4) cannot be correct.
At this point, knowing how the Regents operates, you can be pretty sure that the answer is 60, and that 120 is there in case you forget to multiply by 1/2, a common error.
Doing it this way, you have 132 - (1/2)(11)(3) - (1/2)(9)(7) - (1/2)(12)(4) = 60.
The long way: the length of AD is the square root of ((-6 - 6)2 + (-1 - 3)2)) = SQRT(144 + 16) = SQRT(160)
The length of NP is the square root of ((-3 - 0)2 + (10 - 1)2)) = SQRT(9 + 81) = SQRT(90)
A = (1/2) * SQRT(160) * SQRT(90) = (1/2) * SQRT(14,440) = (1/2)(120) = 60.
16. Triangle ABC, with vertices at A(0,0), B(3,5), and C(0,5), is graphed on the set of axes shown below.
Which figure is formed when ABC is rotated continuously about BC?
Answer: (3) (see image)
When you rotate the triangle, you will get a cone. The axis BC that it is rotated around, will be the altitude of the cone. The base of the triangle will become the radius of the cone.
So the height is 3, the radius is 5 and the diameter is 10. Choice (3).
Note that Choices (1) and (2) are rotated about the wrong line.
17. In the diagram below of circle O, chords AB and CD intersect at E.
If mAC = 72° and m∠AEC = 58°, how many degrees are in mDB ?
Answer: (3) 44°
58 is the average of 72 and mDB.
58 = (72 + x)/2
2(58) = 72 + x
116 - 72 = x
44 = x.
Alternatively, 72 - 58 = 14, and 58 - 14 = 44.
18. In triangle SRK below, medians SC, KE, and RL intersect at M.
Which statement must always be true?
Answer: (1) 3(MC) = SC
The three medians of a triangle meet at a centroid, which is point M. The distance from the angle to the centroid is ALWAYS twice as much as from the centroid to the midpoint of the opposite side. That always means that the distance from the centroid to the midpoint is one-third the length of the entire median. So 3(MC) = SC is always true.
Incorrect choices: (2) MC is 1/3 of SC, not 1/3 of SM; (3) RM is 2 times ML, not MC, which is unrelated to RM; (4) SM and KM could be the same size but there is no reason that they must be.
19. MThe regular polygon below is rotated about its center.
Which angle of rotation will carry the figure onto itself?
Answer: (3) 216°
One full rotation is 360 degrees. A regular pentagon will carry onto itself every 1/5th of a rotation.
360 / 5 = 72 degrees. So this will happen at any multiple of 72 degrees.
72 * 3 = 216.
Incorrect choices: (1) 60 degrees is for a hexagon; (2) 108 degrees is the measure of one interior angle of a regular pentagon; (4) 540 degrees is the total number of degrees of the interior angles.
20. What is an equation of circle O shown in the graph below?
Answer: (2) x2 - 10x + y2 - 4x = -13
The standard form for a circle is (x - h)2 + (y - k)2 = r2, where (h,k) is the center.
The center is (5,2) and the radius is 4, so (x - 5)2 + (y - 2)2 = 42.
The choices are not in standard form, so you have to square the binomials.
x2 - 10x + 25 + y2 - 4x + 4 = 16
x2 - 10x + y2 - 4x = 16 - 25 - 4
x2 - 10x + y2 - 4x = -13
21. In the diagram below of PQR, ST is drawn parallel to PR, PS = 2, SQ = 5, and TR = 5.
What is the length of QR?
Answer: (4) 17.5
The ratio between the side lengths is the same. So if PS = 2 and RT = 5, then QR is 2.5 times the length of PQ. And QR is 2.5 times as long as QP, so 2.5 * 7 = 17.5
Or you can write a proportion to find QT.
5 / 7 = x / (x + 5)
7x = 5(x + 5)
7x = 5x + 25
2x = 25
x = 12.5
If QT = 12.5 and TR = 5, then QR = 12.5 + 5 = 17.5
22. The diagram below shows circle O with radii OA and OB. The measure
of angle AOB is 120°, and the length of a radius is 6 inches.
Which expression represents the length of arc AB, in inches?
Answer: (4) (1/3)(12π)
The length of an arc of the circle is the Circumference (2πr) times the fraction of the central angle divided by 360.
(120/360)(2π)(6) = (120/360)(12π) = (1/3)(12π)
23. Line segment CD is the altitude drawn to hypotenuse EF in right triangle ECF. If EC = 10 and EF = 24, then, to the nearest tenth, ED is
Answer: (1) 4.2
If it helps, draw a diagram.
ED is the shorter leg of right triangle EDC, and EC is the shorter leg of triangle ECF.
EC is the hypotenuse of right triangle EDC, and EF is the hypotenuse of triangle ECF.
Write a proportion:
x / 10 = 10 / 24
24x = (10)(10)
x = 100 / 24 = 4.2
If you draw a diagram, you can see that ED had to be shorter than EC, so choices (3) and (4) make no sense. Eliminate them.
24. Line MN is dilated by a scale factor of 2 centered at the point (0,6). If is MN represented by y = -3x + 6, which equation can represent M'N', the image of MN?
Answer: (2) y = -3x + 6
A dilation would not change the slope of a line, so eliminate Choices (3) and (4).
A dilation would only change the y-intercept UNLESS the line goes through the center of dilation -- that is, if the center of dilation is a point on the line. In that case, the line remains unchanged because the image of every point will still fall on the same line.
Check for this: 6 = -3(0) + 6
6 = 6, which is true, so the center of dilation is on the line, and the image is the same line.
End of Part I
How did you do?
Questions, comments and corrections welcome.
I also write Fiction!Check out In A Flash 2020, by Christopher J. Burke for 20 great flash fiction stories, perfectly sized for your train rides. Available in softcover or ebook at Amazon. If you enjoy it, please consider leaving a rating or review on Amazon or on Good Reads. Thank you. |
 |






























6 comments:
Thanks so much! This really helped me understand why I kept getting some questions wrong. Again Thank You So Much!!!!!
You're welcome. Glad I could help.
on 14, your work came out to be answer 2, but you said answer 1. i am just practicing for an upcoming regents, and i am confused about which is correct.
Good catch. Looks like a weird transcription error as I was typing from a copy of the exam.
The answer is (2) (2,-2) is stated in the work. The Choice listed is incorrect and will be fixed.
Diagram for question 1 is wrong
Fixed.
Thanks for the correction.
Strange that no one noticed that sooner.
Post a Comment