Geometry Problems of the Day (Geometry Regents, January 2014)

Now that I'm caught up with the current New York State Regents exams, I'm revisiting some older ones.

More Regents problems.

Geometry Regents, January 2014

Part I: Each correct answer will receive 2 credits.


26. A circle with the equation (x + 6)² + (y - 7)² = 64 does not include points in Quadrant

1) I
2) II
3) III
4) IV

Answer: 4) IV

Once again, the formula for the equation of a circle is (x - h)² + (y - k)² = r², where (h, k) is the center of the circle, and r is the radius. Note that there are MINUS SIGNS in the formula.

The center of the circle is (-6, 7) which is in Quadrant II, so eliminate that. The radius is equal to the square root of 64, which is 8. If you go 8 units to the right of (-6, 7), you will be at (2, 7), which is in Quadrant I. If you go 8 units below (-6, 7), you will be at (-6, -1), which is in Quadrant III.

You have eliminated Choices (1), (2) and (3), leaving only IV. But you can check this.

If the center stretches from quadrant II to quadrant IV, it has to go past the origin, and (0, 0) would be inside the circle at a distance less than the radius from the center. That would mean:

(0 + 6)² + (0 - 7)² < 64
and therefore 36 + 49 < 64

This is obviously not a true statement, so the circle does not extend in Quadrant IV.

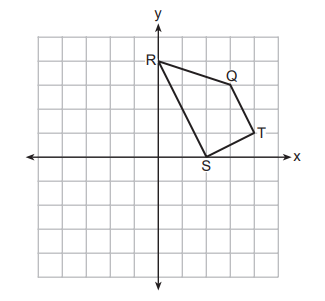
27. Trapezoid QRST is graphed on the set of axes below.

Under which transformation will there be no invariant points?

1) r_{y = 0}
2) r_{x = 0}
3) r_(0,0)
4) r_{y = x}

Answer: 3) r_(0,0)

Invariant points are points on a line or shape which do not move when a specific transformation is applied. Under these transformations, if a point remains in the same place, it is invariant.

In Choice (1), y = 0 is the x-axis. Point S is on the x-axis and will reflect to itself.

In Choice (2), x = 0 is the y-axis. Point R is on the y-axis and will reflect to itself.

In Choice (3), (0,0) means a reflection about the origin. The only put that would remain in place is a point on the origin, but the trapezoid does not pass through the origin. This is the correction answer.

In Choice (4), y = x is a diagonal line through quadrants I and III. It goes through point Q and through an unlabeled point on line RS. Both of those points will reflect onto themselves.

23. How many common tangent lines can be drawn to the circles shown below??

1) 1
2) 2
3) 3
4) 4

Answer: 4) 4

A common tangent line means that the line will be tangent to both circles.

There will be one on top, one on the bottom, and two in-between making an "X". Look at the illustration below:

The radius is the distance from (1, 2) to (-1, 2), which is 2 units. So r = 2, and r² = 4. Eliminate Choices (3) and (4).

Since there are minus signs in the formula, we want (x + 1) and (y - 2) in the equation. That means Choice (2).

More to come. Comments and questions welcome.

More Regents problems.