August 2022 Geometry Regents, Part III

The following are questions from the recent August 2020 New York State Common Core Geometry Regents exam.

August 2022 Geometry, Part III

Each correct answer is worth up to 4 credits. Partial credit can be given. Work must be shown or explained.

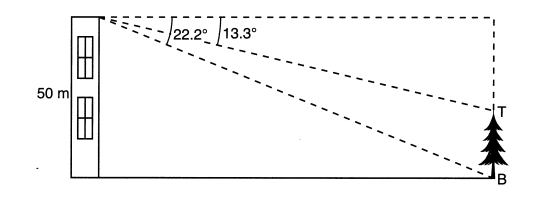
32. As modeled in the diagram below, a building has a height of 50 meters. The angle of depression from the top of the building to the top of the tree, T, is 13.3°. The angle of depression from the top of the building to the bottom of the tree, B, is 22.2°.

Determine and state, to the nearest meter, the height of the tree.

Answer:
You can find the height of the tree if you can find the side opposite the 13.3 degree angle and then subtract that from 50 meters. However, we don't know any sides of that triangle.

On the other hand, we can use the 22.2 degree angle to find the distance from the building to the tree, and then use that to find the height of the tree.

tan 22.2 = 50 / x
x = 50 / tan 22.2 = 122. 5213...

Keep the extra decimals! DO NOT ROUND IN THE MIDDLE OF THE SOLUTION!!

tan 13.3 = y / 122.5213
y = 122.5213 tan 13.3 = 28.9628...

Subtract 50 - 28.9628 = 21.0372 or approximately 21 meters tall.

33. The coordinates of the vertices of quadrilateral HYPE are H(-3,6), Y(2,9), P(8,-1), and E(3,-4).
Prove HYPE is a rectangle. [The use of the set of axes below is optional.]

Answer:

Answer:
To show that a quadrilateral is a rectangle, so that the opposite sides are parallel (ie, same slope) and that the consecutive sides are perpendicular (ie, inverse reciprocal slopes).

You don't have to show that the opposite sides are congruent in length.

Showing that the diagonals are congruent is not enough because it could be an isosceles trapezoid. You would still need to show parallel sides.

Slope of HY = ((9-6) / (2-(-3)) = 3/5

Slope of YP = ((-1-9) / (8-2)) = -10/6 = -5/3

Slope of PE = ((-4-(-1)) / (3-8)) = -3/-5 = 3/5

Slope of EH = ((6-(-4)) / (-3-3) = 10/-6 = -5/3

The opposite sides have the same slope so HY || PE and YP || HE.

HY is perpendicular to YP because (3/5)(-5/3) = -1. The slopes are inverse reciprocals.

Therefore, HYPE is a rectangle.

Note that drawing the figure doesn't do anything for you, except make it easier to find slope by counting the boxes instead of subtracting signed numbers. You still need to justify your statements.

34. A packing box for baseballs is the shape of a rectangular prism with dimensions of 2 ft X 1 ft X 18 in. Each baseball has a diameter of 2.94 inches.

Determine and state the maximum number of baseballs that can be packed in the box if they are stacked in layers and each layer contains an equal number of baseballs.

The weight of a baseball is approximately 0.025 pound per cubic inch. Determine and state, to the nearest pound, the total weight of all the baseballs in the fully packed box.

Answer:
Divide each dimension of the box by 2.94 to see how many whole number of baseballs fit each way. Multiply that number to get the maximum number of baseballs in the box. Then find the Weight of 1 baseball by multiplying the Volume by 0.025. Then multiply that by the number of baseballs you found in the first part.

24/2.94 = 8.2, or 8. 12/2.94 = 4.1 or 4. 18/2.94 = 6.1 or 6.

Since they are all multiples of 6, you could have figured out the 12 inches first and the used proportions for the other two, if you wanted.

# of baseballs = 8 * 4 * 6 = 192. You can have partial baseballs in the box.

r = 1/2 D = 1/2 (2.94) = 1.47

V = (4/3) π r³ = (4/3) π (1.47)³ = 13.3057...

13.3057 * 0.025 = 0.3326

0.3326 * 192 = 63.8592 or about 64 pounds.

Again, be careful about rounding and the number of decimals that you carry in each step of the problem. You could easily go astray with less precision and get 63 or 65 as an answer. You would lose a credit for that.

End of Part III

How did you do?

Questions, comments and corrections welcome.

I also write Fiction! Check out In A Flash 2020, by Christopher J. Burke for 20 great flash fiction stories, perfectly sized for your train rides. Available in softcover or ebook at Amazon. If you enjoy it, please consider leaving a rating or review on Amazon or on Good Reads. Thank you.