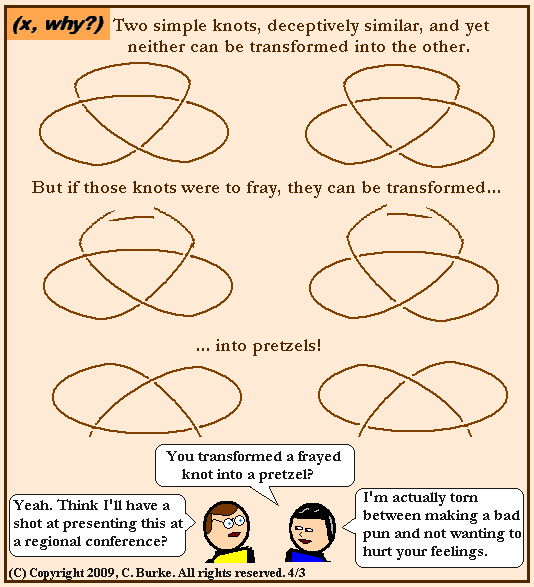
It's that Law of Gravity that's really keeping me down...
By the way, I'm aware that Rich Bond isn't really a money guy. But c'mon! It's just too good a name not to use.
Previous episodes of The 0'Factor: 01, 02, 03, 04, 05, 06, 07, 08, 09.


By the way, I'm aware that Rich Bond isn't really a money guy. But c'mon! It's just too good a name not to use.
Previous episodes of The 0'Factor: 01, 02, 03, 04, 05, 06, 07, 08, 09.





For more on Henry's and Ian's adventures, click on the following links:
Through a Window Darkly: Part I,II,III, IV, V, VI, TVH, TUC.



 follow a pattern
follow a patternP1 = 1, Q1 = 0, Qn+1 = Pn, Pn+1 = 2 X Pn + Qn To follow my method, calculate 1 + Q/P as an improper fraction. As in my prior post, this will give you a triple in the form (a+b)/c, where b = a + 1. This method was "easier" for me than what Kraitchik (1953) wrote, but it required more iterations to get each Pythagorean Triple. Kraitchik offers a shortcut, which is essentially: a = 2PQ and b = P2 - Q2, which yields numbers such that | a - b | = 1 For example: a = 2(2)(1) = 4, b = (2)2 - (1)2 = 3, c = 5 a = 2(5)(2) = 20, b = (5)2 - (2)2 = 21, c = 29 a = 2(12)(5) = 120, b = (12)2 - (5)2 = 119, c = 169 etc. |



 was involved, along with the fraction:
was involved, along with the fraction: , which converges on
, which converges on  .
. would be involved with Pythagorean triples because of the numbers association with right isosceles triangles. As the legs of the triangle increase in size, the ratio of two consecutive numbers comes closer to 1:1.
would be involved with Pythagorean triples because of the numbers association with right isosceles triangles. As the legs of the triangle increase in size, the ratio of two consecutive numbers comes closer to 1:1.    Followed by: 99/70 and 239/169 | If you look at the fractions with the odd denominators, you have a Pythagorean Triple in the form of (a+b)/c, where a and b are consecutive numbers (i.e., b = a + 1) 7/5 gives you 3, 4, 5. 41/29 gives you 20, 21, 29 239/169 gives you 119, 120, 169 |


b = (1/8)a2 - 2 | c = (1/8)a2 + 2 |


| a2 + b2 = (b + 2)2 a2 + b2 = b2 + 4b + 4 a2 = 4b + 4 a2 = 4(b + 1) 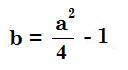 | c = b + 2 c = (1/4)a2 - 1 + 2 c = (1/4)a2 + 1 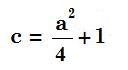 |
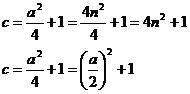




| a2 + b2 = (b + 1)2 a2 + b2 = b2 + 2b + 1 a2 = 2b + 1 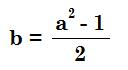 | c = b + 1 c = (1/2)(a2 - 1) + 1 c = (1/2)(a2 + 1) 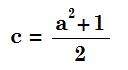 |
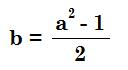




 Squares can be made by summing consecutive odd numbers. When that addend is a perfect square, the result is a Pythagorean Triple.
Squares can be made by summing consecutive odd numbers. When that addend is a perfect square, the result is a Pythagorean Triple.