Geometry Problems of the Day (Geometry Regents, June 2011)

Now that I'm caught up with the current New York State Regents exams, I'm revisiting some older ones.

More Regents problems.

Geometry Regents, June 2011

Part III: Each correct answer will receive 4 credits. Partial credit is available.


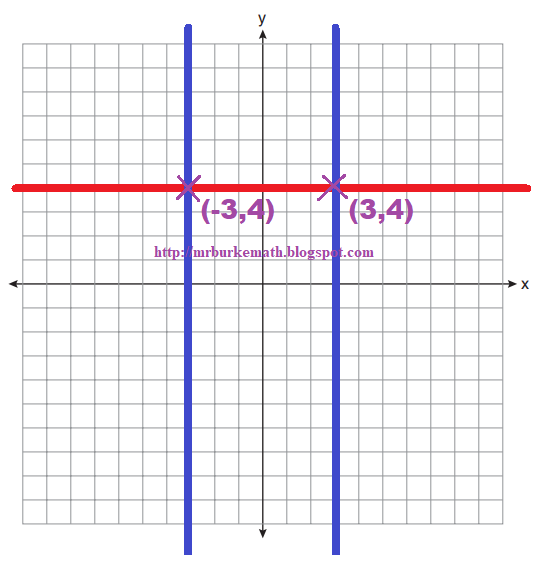
35. On the set of coordinate axes below, graph the locus of points that are equidistant from the lines y = 6 and y = 2 and also graph the locus of points that are 3 units from the y-axis. State the coordinates of all points that satisfy both conditions.

Answer:

The locus of points equidistant from horizontal lines y = 6 and y = 2 is the horizontal line y = 4, which is right in the middle of it. The locus of points 3 units from the y-axis is two vertical lines at x = 3 and x = -3.

The vertical lines intersect the horizontal line at (-3,4) and (3,4).

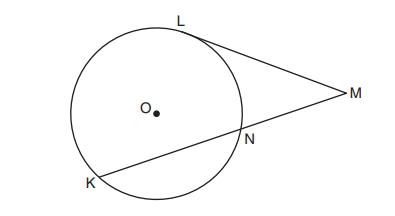
36. In the diagram below, tangent ML and secant MNK are drawn to circle O. The ratio mLN : mNK : mKL is 3:4:5. Find m∠LMK.

Answer:

If the circle is divided into three arcs, then those three arcs must add up to 360 degree. If they are in the ratio of 3:4:5, then the following is true;

3x + 4x + 5x = 360

12x = 360

x = 30

This means that mLN = 3(30) = 90, mNK = 4(30) = 120, and mKL = 5(30) = 150.

The measure of angle LMK is (mKL - mLN) / 2 = (150 - 90) / 2 = 60 / 2 = 30 degrees.

37. Solve the following system of equations graphically.

2x² − 4x = y + 1

x + y = 1

Answer:

Graph and label both lines. Label the points of intersection, and state the coordinates.

Rewrite the quadratic equation as y = 2x² - 4x - 1, and the linear equation as y = -x + 1.

The Axis of Symmetry of the parabola is x = -(-4)/(2(2)) = 1. When x = 1, y = 2(1)² - 4(1) - 1 = -3, so the vertex is (1,-3). You can start plotting points from there.

Your graph should look like the one below:

You may want to check on your calculator that 2(-1/2)² - 4(-1/2) = (3/2) + 1 because you can't really go by "looks".

2(-1/2)² - 4(-1/2) = 5/2

3/2 + 1 = 5/2

End of Part III.

More to come. Comments and questions welcome.

More Regents problems.

I also write Fiction! You can now preorder Devilish And Divine, edited by John L. French and Danielle Ackley-McPhail, which contains (among many, many others) three stories by me, Christopher J. Burke about those above us and from down below. Preorder the softcover or ebook at Amazon. Also, check out In A Flash 2020, by Christopher J. Burke for 20 great flash fiction stories, perfectly sized for your train rides. Available in softcover or ebook at Amazon. If you enjoy it, please consider leaving a rating or review on Amazon or on Good Reads.