If you don't get this, maybe you're not a diamond. Maybe you're just a square.
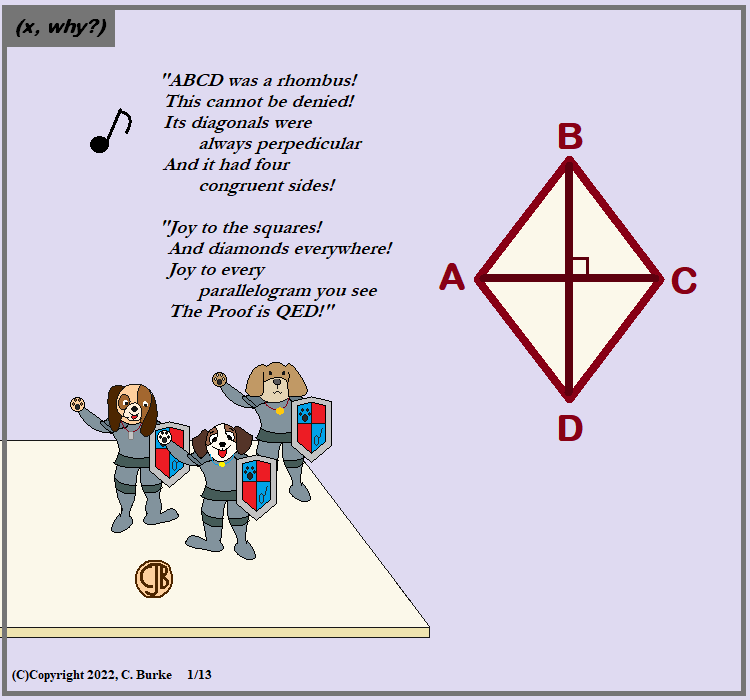
Parallelograms have diagonals that bisect each other. This goes for every subclass.
Rhombuses (rhombi) take it a step further and have diagonals that are perpendicular bisectors. This means that by SSS (or HL, if you prefer), the diagonals divide the rhombus into four congruent triangles.
Flipping the problem sideways, if you start with diagonals perpendicularly bisect each other, you can prove that the quadrilateral is a rhombus using SAS and CPCTC to show that the four sides of the quadrilateral must be congruent to each other.
Sometimes Geometry proofs can be fun ... and sometimes you have to write them out precisely, taking some of the full out of it.
Bonus Comic
As you may know, I sometimes give the "official" answers to Calendar Math problems, and sometimes I do this by making a comic out the answer. Another one will be included here later today.
I also write Fiction!You can now Preorder the softcover or ebook at Amazon. Also, check out In A Flash 2020, by Christopher J. Burke for 20 great flash fiction stories, perfectly sized for your train rides. Available in softcover or ebook at Amazon. If you enjoy it, please consider leaving a rating or review on Amazon or on Good Reads. |
 |
 |
Come back often for more funny math and geeky comics.

















No comments:
Post a Comment