More Algebra 2 problems.
January 2018
If G(t) is the average price of gas in dollars and t represents the number of months since January 1st, the absolute maximum G(t) reaches over the given domain is about
17. The function below models the average price of gas in a small town computations.
since January 1st.
G(t) = -0.0049t4 + 0.0923t3 - 0.56t2 + 1.166t + 3.23,
where 0 ≤ t ≤ 10.
(1) $1.60
(2) $3.92
(3) $4.01
(4) $7.73
Answer: (3) $4.01
Graph the function and use "maximum" to find the highest value, which you should see is just above $4.00.
See the graph below:
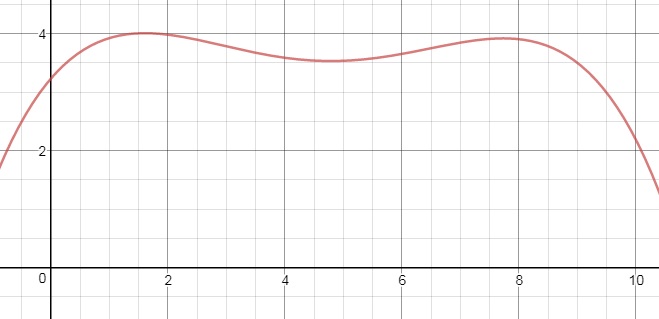
At approximately t = 1.6, G(t) = 4.01, approximately.
18. Written in simplest form, (c2 - d2) / (d2 + cd - 2c2), where c =/= d, is equivalent to
(1) (c + d) / (d + 2c)
(2) (c - d) / (d + 2c)
(3) (-c - d) / (d + 2c)
(4) (-c + d) / (d + 2c)
Answer: (3) (-c - d) / (d + 2c)
The numerator, (c2 - d2), is the difference of two perfect squares, and factors into the conjugates, (c + d)(c - d).
Note that all four choices have (d + 2c) as the denominator, which makes factoring (d2 + cd - 2c2) that much easier into (d + 2c)(d - c).
(c - d) / (d - c) = -1, which reduces the fraction to (-1)(c + d) / (d + 2c).
Distribute the -1, and you get choice (3).
Comments and questions welcome.
More Algebra 2 problems.

















2 comments:
Can you please explain how did you get to your answer on 17. How did you get to the graph? I tried working out the numbers for max t of 10 and my solution was 2.19
The image was taken from Desmos graphing calculator, but any graphing calculator will give a similar image.
The highest y-value (the value of G(t) ) is a little more than 4, which occurs when t is about 1.6.
Why did you evaluate t = 10? That isn't where the maximum value is.
Post a Comment