Now that I'm caught up with the current New York State Regents exams, I'm revisiting some older ones. The Integrated Algebra Regents covered most of the same material as the current Algebra Regents, with a few differences.
More Regents problems.
Integrated Algebra Regents, August 2010
Part IV: Each correct answer will receive 4 credits. Partial credit is available. One computational error will cost 1 credit. A conceptual error will usually cost 2 credits.
State the coordinates of a point in the solution set.
37. On the set of axes below, solve the following system of inequalities graphically.
y ≥ −1/3 x + 4
Answer:
The inequalities are already in slope-intercept form, making them easy to graph without a calculator or even a table of values. (You can make a table of values if you want to.)
A "less than" sign means that the line will be broken/dashed, and the shading will go beneath the line. Any points on that line are NOT points in the solution set.
A "greater than or equal to" sign means that the line will be solid, and the shading will go above the line. Any points on that line are solutions to this inequality, but not necessarily to the entire system.
The solution set to the system is the section of the graph that is shaded twice.
Pick any point in the double-shaded area, such as: (5,5).
If a student were to randomly pick one marble from each of these three hats, determine from
which hat the student would most likely pick a green marble. Justify your answer.
Determine the fewest number of marbles, if any, and the color of these marbles that could be
added to each hat so that the probability of picking a green marble will be one-half in each of the
three hats.
38. Each of the hats shown below has colored marbles placed inside. Hat A contains five green
marbles and four red marbles. Hat B contains six blue marbles and five red marbles. Hat C contains
five green marbles and five blue marbles.
Answer:
For the first part, you have to determine P(green) for each hat. Then state which hat has the greatest P(green). (Note that there are NO green marbles in Hat B.) For the second part, if any hat has less P(green) < 1/2, how many green marbles need to be added to make the probability equal 1/2. If any hat has P(green) > 1/2, how many marbles of a different color would need to be added.
Hat A: P(Green) = 5 / (5+4) = 5/9
Hat B: P(Green) = 0. (There are no green marbles in Hat B.)
Hat C: P(Green) = 5 / (5+5) = 5/10 = 1/2.
Hat A has the greatest probability of selecting a green marble.
Part 2:
Hat A: Add 1 red (or any non-green) marble and there will be 5 green and 5 red. P(Green) = 1/2.
Hat B: There are 11 marbles in the hat. Add 11 green marbles and P(Green) = 11/22 = 1/2.
Hat C: Do not add any marbles.
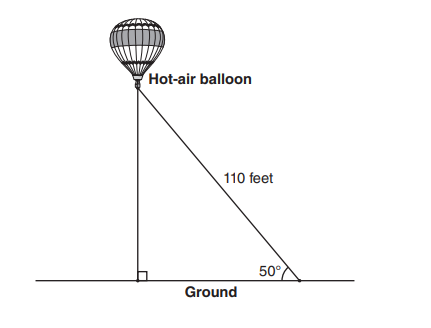
Determine the height, to the nearest foot, of the balloon directly above the ground/
Determine the distance, to the nearest foot, on the ground between the two ropes.
39. A hot-air balloon is tied to the ground with two taut (straight) ropes, as shown in the diagram
below. One rope is directly under the balloon and makes a right angle with the ground. The other
rope forms an angle of 50° with the ground.
Answer:
The height above the ground is the side opposite the angle. You have the length of the rope, with is the hypotenuse of the triangle. Therefore, to find the height, you need to use the Sine ration.
To find the distance on the ground, you have three choices: you can use the cosine ration, the tangent ratio, or Pythagorean Theorem.
Height: sin 50 = x / 110
x = 110 sin 50 = 84.26..., or 84 feet.
Distance on the ground:
a) cos 50 = x / 110
x = 110 cos 50 = 70.70..., or 71 feet.
b) tan 50 = 110 / x
x = 84 / tan 50 = 70.48..., or 70 feet -- If you did this, they would have to accept your answer because you used the answer from part 1, rounded the way that you were told to.
(I am not 100% certain of that, but some scorer should've been arguing in your favor.)
c) x2 + 842 = 1102
x2 + 7056 = 12100
x2 = 5044
x = 71.02..., or 71 feet.
End of Part Exam. How did you do?
More to come. Comments and questions welcome.
More Regents problems.
I also write Fiction!You can now order Devilish And Divine, edited by John L. French and Danielle Ackley-McPhail, which contains (among many, many others) three stories by me, Christopher J. Burke about those above us and from down below. Order the softcover or ebook at Amazon. Also, check out In A Flash 2020, by Christopher J. Burke for 20 great flash fiction stories, perfectly sized for your train rides. Available in softcover or ebook at Amazon. If you enjoy it, please consider leaving a rating or review on Amazon or on Good Reads. |
 |
 |


















No comments:
Post a Comment