Geometry Problems of the Day (Geometry Regents, January 2013)

Now that I'm caught up with the current New York State Regents exams, I'm revisiting some older ones.

More Regents problems.

Geometry Regents, June 2013

Part I: Each correct answer will receive 2 credits.


6. 6 Plane A and plane B are two distinct planes that are both perpendicular to line ℓ. Which statement about planes A and B is true?

1) Planes A and B have a common edge, which forms a line
2) Planes A and B are perpendicular to each other.
3) Planes A and B intersect each other at exactly one point.
4) Planes A and B are parallel to each other.

Answer: 4) Planes A and B are parallel to each other.

Think of a floor and a ceiling and an elevator shaft that is perpendicular to the two of them. The floor and ceiling are parallel to each other and perpendicular to the elevator shaft.

Planes A and B will not intersect. If they were perpendicular to each other, they would have a common edge, which would form a line. So (2) couldn't be true without (1) also being true.

Choice (3) makes no sense. Two planes cannot meet at a single point.

7. Triangle ABC is similar to triangle DEF. The lengths of the sides of ABC are 5, 8, and 11. What is the length of the shortest side of DEF if its perimeter is 60?

1) 10
2) 12.5
3) 20
4) 27.5

Answer: 2) 12.5

The sides of similar triangles are proportional and so are the perimeters. If one triangle has a perimter of 5 + 8 + 11 = 24 and the other triangle has a perimeter of 60, then the scale factor between the two is 60/24 or 5/2.

The shortest side of the smaller triangle is 5 so the shortest side of the bigger triangle must be 5 * 5/2 = 12.5

3. In the diagram below of right triangle ABC, altitude CD is drawn to hypotenuse AB.

If AD = 3 and DB = 12, what is the length of altitude CD?

1) 6
2) 6 SQRT(5)
3) 3
4) 3 SQRT(5)

Answer: 1) 6

The Right Triangle Altitude Theorem says that (AD)(DB) = (CD)².

(3)(12) = (AD)²
36 = (AD>²
AD = 6

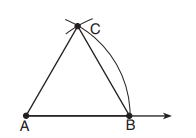
9. The diagram below shows the construction of an equilateral triangle.

Which statement justifies this construction?

1) ∠A + ∠B + ∠C = 180
2) m∠A = m∠B = m∠C
3) AB = AC = BC
4) AB + BC > AC

Answer: 3) AB = AC = BC

The construction is completed using the length of AB to create AC and BC.

The other choices are all true statements but have nothing to do with the construction of the equilateral triangle.

10. What is the slope of the line perpendicular to the line represented by the equation 2x + 4y = 12?

1) -2
2) 2
3) -1/2
4) 1/2

Answer: 2) 2

To find the slope of the line perpendicular to the given line, you first need the slope of the given line.

The given line is in Standard Form, Ax + By = C, and the slope is -A/B, or -2/4 = -1/2.

If you didn't realize this, you can rewrite it in slope-intercept form:
2x + 4y = 12
4y = -2x + 12
y = -1/2 x + 3

A line perpendicular to a line with a slope of -1/2 would have a slope of 2 because that is the inverse reciprocal and because (-1/2)(2) = -1.

More to come. Comments and questions welcome.

More Regents problems.

I also write Fiction! You can now preorder Devilish And Divine, edited by John L. French and Danielle Ackley-McPhail, which contains (among many, many others) three stories by me, Christopher J. Burke about those above us and from down below. Preorder the softcover or ebook at Amazon. Also, check out In A Flash 2020, by Christopher J. Burke for 20 great flash fiction stories, perfectly sized for your train rides. Available in softcover or ebook at Amazon. If you enjoy it, please consider leaving a rating or review on Amazon or on Good Reads.