More Algebra 2 problems.
January 2020, Part I
All Questions in Part I are worth 2 credits. No work need be shown. No partial credit.
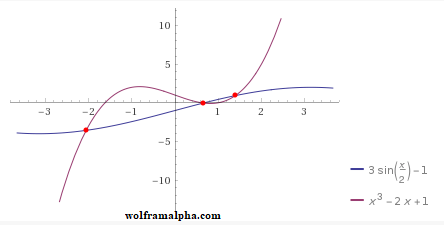
21. Which value, to the nearest tenth, is the smallest solution of f(x) = g(x) if f(x) = 3sin( 1/2 x) - 1 and g(x) = x3 - 2x + 1?
(1) -3.6
(2) -2.1
(3) -1.8
(4) 1.4
Answer: (2) -2.1
Put both equations in your graphing calculator. You should be able to see the results clearly enough to pick the correct choice. However, if you do not, you can use the Calculator functions. (2nd TRACE, option 5, on TI-83 and beyond)
22. Expressed in simplest a + bi form, (7 - 3i) + (x - 2i)2 - (4i + 2x2) is
(1) (3 - x2) - (4x + 7)i
(2) (3 + 3x2) - (4x + 7)i
(3) (3 - x2) - 7i
(4) (3 + 3x2) - 7i
Answer: (1) (3 - x2) - (4x + 7)i
(7 - 3i) + (x2 - 4xi + 4i2) - (4i + 2x2)
x2 - 2x2 + 7 - 4 - 3i - 4i - 4xi
-x2 + 3 - 7i - 4xi
(3 - x2) - (4x + 7)i
23. Written in simplest form, the fraction (x3 - 9x)/(9 - x2), where x =/= 3, is equivalent to
<
(1) -x
(2) x
(3) -x(x + 3) / (3 + x)
(4) x(x - 3) / (3 - x)
Answer: (1) -x
You should immediately realize that neither (3) nor (4) are in simplest term. In (3), the two binomials are the same, which results in 1. In (4), (x - 3)/(3 - x) reduce to -1.
(x3 - 9x)/(9 - x2)
(x)(x2 - 9)/(9 - x2)
(x)(-1)(9 - x2)/(9 - x2)
-x
Solve for y: (4) + y + (11) = 9
y + 15 = 9
y = -6
24. According to a study, 45% of Americans have type O blood. If a random
number generator produces three-digit values from 000 to 999, which
values would represent those having type O blood?
(1) between 000 and 045, inclusive
(2) between 000 and 444, inclusive
(3) between 000 and 449, inclusive
(4) between 000 and 450, inclusive
Answer: (3) between 000 and 449, inclusive
45% of 1,000 numbers is 450
Including 000 means that the 450th number would be 449.
Comments and questions welcome.
More Algebra 2 problems.

















No comments:
Post a Comment