Geometry Problems of the Day (Geometry Regents, June 2011)

Now that I'm caught up with the current New York State Regents exams, I'm revisiting some older ones.

EDIT: I don't know what exam I started below, but it doesn't appear to be August 2011. It will be corrected soon.

More Regents problems.

Geometry Regents, June 2011

Part I: Each correct answer will receive 2 credits.


6. In the diagram below, line p intersects line m and line n.

If m∠1 = 7x and m∠2 = 5x + 30, lines m and n are parallel when x equals

1) 12.5
2) 15
3) 87.5
4) 105

Answer: 2) 15

It should be pretty obvious from the Choices that (3) and (4) are the angle sizes and that either (1) or (2) is the value of x we want.

Angles 1 and 2 are congruent because they are alternate interior angles. They are NOT supplementary. So you want to write an equation that says that they are equal to each other, not one that sums them to 180.

7x = 5x + 30

2x = 30

x = 15

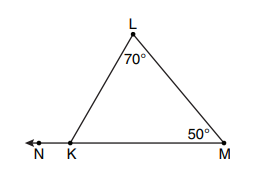
7. In the diagram of △KLM below, m∠L = 70, m∠M = 50, and MK is extended through N.

What is the measure of ∠LKN ?

1) 60°
2) 120°
3) 180°
4) 300°

Answer: 2) 120°

Choices (3) and (4) are just bizarre. Cross them out immediately.

The Remote Angle Theorem tells you that ∠LKN is the sum of the two given angles, 70 + 50 = 120.

If you didn't remember that theorem, you could do it the long way: angle LKM must be 60 degrees, because the three angles of a triangle must add up to 180. Then LKN must be supplementary to the 60 degree angle, and 180 - 60 = 120. Same result. Choice (2).

8. If two distinct planes, A and B, are perpendicular to line c, then which statement is true?

1) Planes A and B are parallel to each other.
2) Planes A and B are perpendicular to each other.
3) The intersection of planes A and B is a line parallel to line c.
4) The intersection of planes A and B is a line perpendicular to line c.

Answer: 1) Planes A and B are parallel to each other.

Consider a fire pole from floor 2 to floor 1 in a firehouse. Or consider an elevator, but that isn't as much fun as a fire pole.

You can also think of a a line running across a floor from one wall to a parallel wall opposite it. Or a shoebox. Or anything similar. The planes will not intersect each other.

9. What is the length of the line segment whose endpoints are A(−1,9) and B(7,4)?

1) √(61)
2) √(89)
3) √(205)
4) √(233)

Answer: 2) √(89)

Use Pythagorean Theorem or the Distance Formula. (You can make a sketch on the scratch graph paper and count the boxes. Whichever.)

From -1 to 7 is a distance of 8 units. From 9 to 4 is a distance of 5 units. (This is length, so we don't want a negative sign).

8^2 = 64 and 5^2 = 25; and 64 + 25 = 89.

So the length is √(89).

10. What is an equation of circle O shown in the graph below?

1) (x + 1)² + (y − 3)² = 25
2) (x - 1)² + (y + 3)² = 25
3) (x - 5)² + (y + 6)² = 25
4) (x + 5)² + (y − 6)² = 25

Answer: 1) (x + 1)² + (y − 3)² = 25

The equation for a circle is given by the formula (x - h)² + (y - k)² = r², where (h,k) is the center of the circle and r is the radius.

The center of the circle is (-1,3), so eliminate Choices (3) and (4). Since there are minus signs in the formula, the signs get flipped. The -1 becomes (x + 1) and the 3 becomes (x - 3). This is Choice (1).

Since r² is 25 is all four choices, you don't have to calculate the radius from the two points.

More to come. Comments and questions welcome.

More Regents problems.

I also write Fiction! You can now preorder Devilish And Divine, edited by John L. French and Danielle Ackley-McPhail, which contains (among many, many others) three stories by me, Christopher J. Burke about those above us and from down below. Preorder the softcover or ebook at Amazon. Also, check out In A Flash 2020, by Christopher J. Burke for 20 great flash fiction stories, perfectly sized for your train rides. Available in softcover or ebook at Amazon. If you enjoy it, please consider leaving a rating or review on Amazon or on Good Reads.