When I was first started creating comics to post to my blog (which actually started a year and a half before I scribbled those Co-Medians in MS-Paint), one of my earliest attempts at Punnery was this comic about Transcendental Numbers
Link to comic page.
One thing that I never answered in the blog -- because I really didn't use the comic as an opportunity for learning at the time -- was just what is a transcendental number? (I could make another joke right now, but I'm writing on a notepad to use at a later date.)
Transcendental numbers are a type of Irrational number, but they aren't the same. In fact, when I create that "What Kind of Numbers Are There?" Venn diagram on the first day of Algebra class, I could actually include a subset circle on the Irrational side. (But, I don't for reasons similar to why I don't have an Imaginary oval next to the Real one. It's not going to matter any time soon.)
There are a lot of Irrational numbers (as we discussed a few days ago in a different post), including square roots of non-perfect squares. Those numbers aren't transcendental. Which numbers "transcend" these ordinary irrationals?
The definition of a Transcendental number is any number that is NOT Algebraic. Don't you just love negative definitions? Anyway, an Algebraic number is one that can be the root of a polynomial equation (such as a quadratic equation) which has only rational coefficients. Since x2 - 2 = 0 has rational coefficients, its roots -- plus or minus radical two -- are Algebraic. But some numbers cannot be roots of these equations. Which ones?
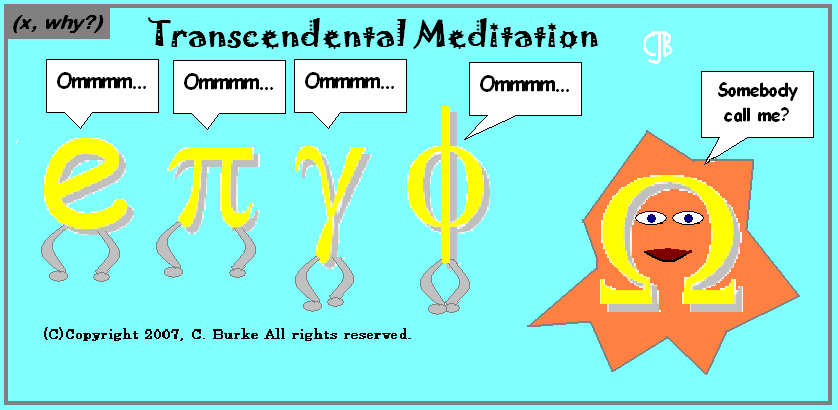
As the cartoon suggests, pi and e are two examples. The third one, gamma, is the Euler–Mascheroni constant (also called Euler's constant), which is found in Number Theory, and which I freely admit I was completely unaware of before 2008 when I looked up transcendental numbers to make the comic (and earlier this evening when I wanted to write this entry).
The last is phi (pronounced "fee"), which I've mentioned before in the blog and in the comics, which is related to the Golden Ratio. This has the distinction of being incorrect, but I'm not updating it eight years after the fact. I read some information back then that some considered it to be one for whatever properties, so I used it because I had a comic to make. However, according to the definition I used above, it can't be transcendental because it is the root of x2 - x - 1 = 0. (What other definitions or properties are out there? That is left an exercise for the reader to ascertain, if you really want to.)
Finally, closing out the joke with a further pun, because it is "Transcendental Meditation", each of the characters (with their little legs are cross as they could go) are saying "Ommmm....", which sounds like "Ohm", which is a unit of Resistance, which uses the letter omega. What I actually knew at the time because I had just read a book about it the previous summer, was that omega was actually the symbol for Chaitlin's constant, which -- drumroll -- is irrational and transcendental.
Seriously, I really did know about this, even if I was, at the time, a little fuzzy on what a transcendental number was. But, at least, now you're not.

Phi is an algebraic number and for gamma it is not known yet if it is irrational or not
ReplyDelete